Cho hàm số y = (m - 1)x + 2 - m ( với m khác 1 ) (1) có đồ thị là (d)
a) tìm m để hàm số (1) đồng biến
b) tìm m để (d) đi qua điểm A(-1 ; 2)
c) tìm m để (d) song song với đồ thị hàm số y = 3x - 11
d) tìm điểm cố định mà (d) đi qua với mọi m ?
Các bạn giải gấp cho mk bài này nha . Mk đang cần rất gấp bạn nào giải đúng mk tick cho

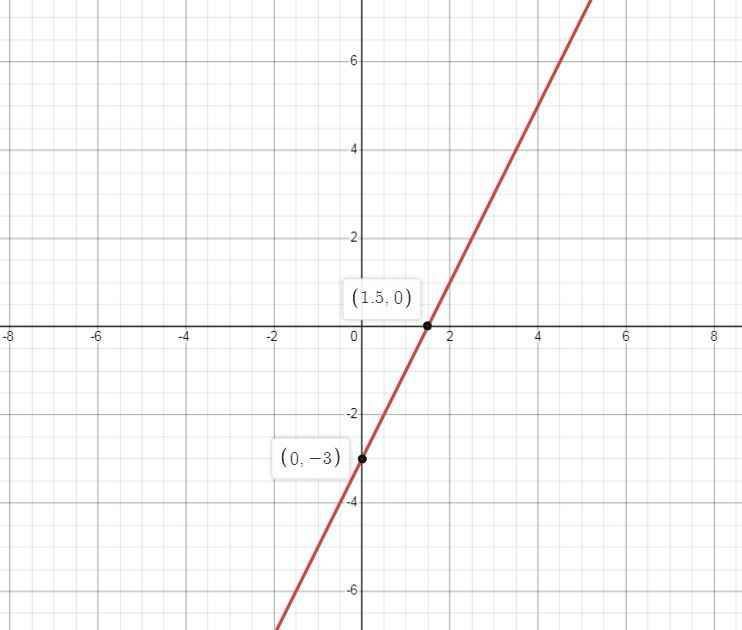
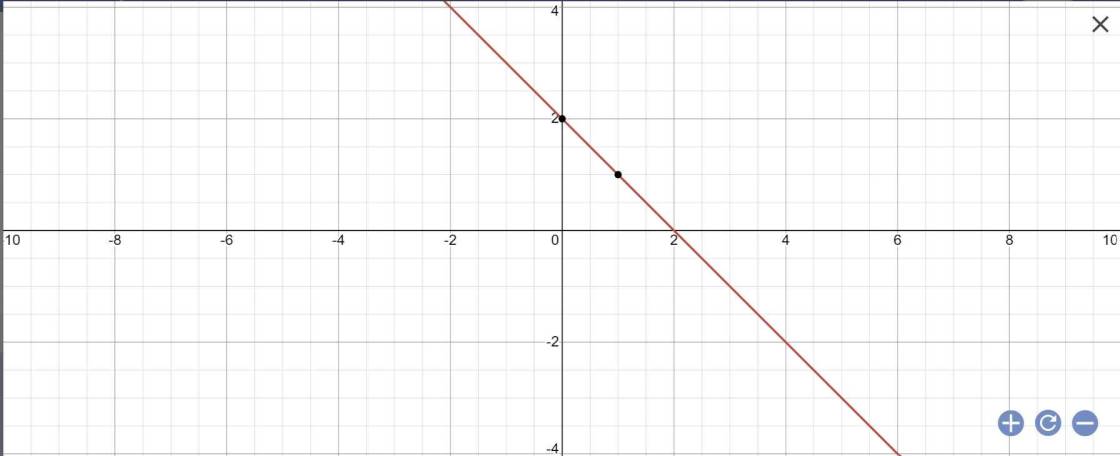 c: y=(m-1)x+2-m
c: y=(m-1)x+2-m
a) Để hàm số (1) đồng biến thì \(m-1>0\Leftrightarrow m>1\)
b) *Với bài như phần b này thì cứ thay x = -1; y = 2 vào phương trình của hàm số là xong*
Để (d) đi qua điểm A(-1 ; 2) thì :
\(2=-\left(m-1\right)+2-m\Leftrightarrow2=3-2m\Leftrightarrow m=\frac{1}{2}\)
c) Để (d) song song với đồ thị hàm số y = 3x - 11 thì \(m-1=3\Leftrightarrow m=4\)
d) \(y=\left(m-1\right)x+2-m=mx-x+2-m=\left(m-1\right)\left(x-1\right)+1\)
Ta thấy với x = 1 thì y = 1.
Vậy điểm cố định cần tìm là B(1 ; 1)
a.Để hàm số (1) đồng biến thì m-1>0
=> m>1
b.A(-1;2)
=> x=-1 ; y=2
Thế vào hàm số y ta được:
2=(m-1)*-1+2-m
<=> 2=-m+1+2-m
<=> 2=-2m+3
<=> -1=-2m
<=> m=1/2
c.Điều kiện để(d)song song với đồ thị hàm số y=3x-11 là:
_m-1=3
<=> m=4 (1)
_2-m khác -11
<=> -m khác -13
<=> m khác 13 (2)
Từ (1) và (2)
=> m=4
d.Giả sử đồ thị hàm số (d) đi qua m
_ta có:
y=(m-1)x+2-m
<=> y=mx-x+2-m
<=> (x-1)m= y+x-2
<=> x-1=0 và y+x-2=0
<=> x=1 ; y=1