cho tam giác ABC có trọng tâm G ( 2; 1 ) và phương trình các đường thẳng : AB : 2x + y - 4 = 0, AC : x - y + 1 = 0. Tìm tọa độ các điểm A, B, C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 7 2023
Tọa độ G là;
\(\left\{{}\begin{matrix}x=\dfrac{4+2+0}{3}=2\\y=\dfrac{0-4-2}{3}=-2\end{matrix}\right.\)
Tọa độ M là:
x=(2+0)/2=1 và y=(-4-2)/2=-3
Tọa độ N là:
x=(4+0)/2=2 và y=(0-2)/2=-1
Tọa độ P là;
x=(4+2)/2=3 và y=(0-4)/2=-2
Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2+3}{3}=2\\y=\dfrac{-3-1-2}{3}=-2\end{matrix}\right.\)
=>Tam giác ABC và tam giác MNP có chung trọng tâm
17 tháng 9 2023
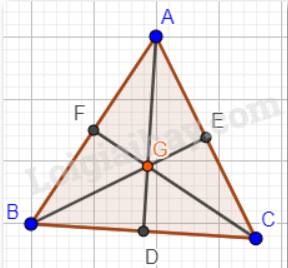
Tam giác ABC đều nên AB = AC = BC.
G là trọng tâm tam giác ABC nên AD, BE, CF là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD.
Xét tam giác ADB và tam giác ADC có:
AB = AC (tam giác ABC đều);
AD chung
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.c.c) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà ba điểm B, D, C thẳng hàng nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \)hay \(AD \bot BC\). (1)
Tương tự ta có:
\(\widehat {AEB} = \widehat {CEB} = 90^\circ \) hay\(BE \bot AC\). (2)
\(\widehat {AFC} = \widehat {BFC} = 90^\circ \) hay\(CF \bot AB\). (3)
Từ (1), (2), (3) suy ra G là giao điểm của ba đường cao AD, BE, CF.
Vậy G cũng là trực tâm của tam giác ABC.
CM
7 tháng 4 2019
Phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F ⇒ biến tam giác ABC thành tam giác DEF.
Đáp án B
CM
6 tháng 12 2018
* Do đỉnh C thuộc trục Ox nên C(a;0).
G thuộc trục Oy nên G(0; b).
* G là trọng tâm tam giác ABC nên:
x G = x A + x B + x C 3 y G = y A + y B + y C 3 ⇒ 0 = − 2 + 6 + a 3 b = 2 + ( − 4 ) + 0 3 ⇔ a = − 4 b = − 2 3
Tọa độ trọng tâm tam giác ABC là G 0 ; − 2 3
Đáp án B
A là giao điểm AB và AC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}2x+y-4=0\\x-y+1=0\end{matrix}\right.\) \(\Rightarrow A\left(1;2\right)\)
Do B thuộc AB nên tọa độ có dạng: \(B\left(b;4-2b\right)\)
Do C thuộc AC nên tọa độ có dạng: \(C\left(c;c+1\right)\)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}1+b+c=3.2\\2+4-2b+c+1=3.1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b+c=5\\-2b+c=-4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=3\\c=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}B\left(3;-2\right)\\C\left(2;3\right)\\\end{matrix}\right.\)