Cho hàm số f(x) liên tục trên ℝ và ∫ 0 1 f ( x ) d x = 2 ; ∫ 0 3 f x d x = 6 . Tính I = ∫ - 1 1 f 2 x - 1 d x ?
A. I = 2 3
B. I = 4
C. I = 3 2
D. I = 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có:
9 = ∫ 0 9 f x d x = F x = 0 9 F 9 = F 0 ⇒ F 9 = F 0 + 9 = 12.

Đặt g ( x ) = 3 f ( x ) - x 3 . Hàm số ban đầu có dạng y=|g(x)|
Ta có g ' ( x ) = 3 f ' ( x ) - 3 x 2 .
Cho g'(x)=0 ⇔ [ x = 0 x = 1 x = 2

Dễ thấy g(0)=0. Ta có bảng biến thiên
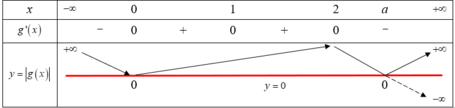
Dựa vào BBT suy ra hàm số y=|g(x)| đồng biến trên khoảng (0;2) và a ; + ∞ với g(a)=0
Chọn đáp án C.
Đáp án B.
Đặt t = 2 x - 1 ⇔ d t = 2 d x và đổi cận x = - 1 ⇒ t = - 3 x = 1 ⇒ t = 1
Khi đó I = 1 2 ∫ - 3 1 f t d t = 1 2 ∫ - 3 0 f - t d t + 1 2 ∫ 0 1 f t d t = 1 2 ∫ 0 3 f ( t ) d t + ∫ 0 1 f t d t = 4 .