Cho hình vẽBiết C F E ^ = 60 o

PT

Pham Trong Bach

31 tháng 7 2017

Cho hình vẽBiết C F E ^ = 60 o ; E 1 ^ = 120 o A. B E F ^ = 60 ° B. AB || CD C. Cả A,B đều đúng D. Cả A,B...

Đọc tiếp

#Toán lớp 7

1

CM

Cao Minh Tâm

31 tháng 7 2017

Đúng(0)

O

★彡✿ทợท彡★

15 tháng 4 2022

Cho 3 tia Ox,Oy,Oz như hình vẽ

biết $\widehat{xOy}=60^o;\widehat{xOz}=80^o$

a) Kể tên các góc trong hình

b) Đo góc $zOy$( phần này bỏ qua cũng được nhé )

c) Vẽ tia Ot là tia đối của tia Ox. So sánh số đo hai góc $zOt$ và $yOt$

z y x O

Giúp với làm đc cho 5 -> 10 coin :))

#Toán lớp 6

1

TC

TV Cuber

15 tháng 4 2022

a) góc zOx

góc yOz

góc xOy

b)ta có $\widehat{yOt}=\widehat{zOy}+\widehat{zOt}>\widehat{zOy}$ O z y x t

Đúng(2)

O

★彡✿ทợท彡★

15 tháng 4 2022

phần b) là c) ak

Đúng(2)

CC

Changg changg

10 tháng 10 2021

Cho hình vẽ

Biết Ax // By

Tính góc ACB

Trả lời gấp hộ mink vs

iu các pạn nhìu u3333

#Toán lớp 7

1

TH

Tô Hà Thu

10 tháng 10 2021

hình vẽ

Đúng(0)

TT

Thầy Tùng Dương

VIP

6 tháng 4 2021 - olm

Trên các cạnh AB, BC, CD và DA của hình vuông ABCD ta lấy lần lượt các điểm E, F, G, H sao cho AE = BF = CG = DH. Các đường chéo AC và BD cắt nhau ở O.

a) Chứng minh rằng ba điểm F, O, H thẳng hàng.

b) Chứng minh rằng điểm O cách đều bốn điểm E, F, G, H.

c) Biết $\widehat{BEC}={60}^\circ$, BC=6cm, tính BE.

#Toán lớp 9

138

C

Cảnh

15 tháng 8 2021

a) Chứng minh được BF = DH \Rightarrow⇒ BFDH là hình bình hành (vì BF // DH). Do đó O thuộc FH (vì O phải là giao điểm của hai đường chéo).

b) Dễ thấy \Delta BEF=\Delta CFGΔBEF=ΔCFG (cgv – cgv) nên EF = FG.

Tương tự, FG = GH, GH = HE \Rightarrow⇒ EF = FG = GH = HE. Suy ra EFGH là hình vuông.

Tương tự phần a) ta chứng minh được O thuộc EG. Từ đó, O là giao điểm hai đường chéo của hình vuông EFGH nên O cách đều E, F, G, H.

c) BE=BC .\cot{{60}^\circ}=\frac{6\sqrt3}{3}=2\sqrt3BE=BC .cot60∘=363=23.

Đúng(0)

PV

Phương Vy

17 tháng 8 2021

a) Chứng minh được BF = DH \Rightarrow⇒ BFDH là hình bình hành (vì BF // DH). Do đó O thuộc FH (vì O phải là giao điểm của hai đường chéo).

b) Dễ thấy \Delta BEF=\Delta CFGΔBEF=ΔCFG (cgv – cgv) nên EF = FG.

Tương tự, FG = GH, GH = HE \Rightarrow⇒ EF = FG = GH = HE. Suy ra EFGH là hình vuông.

Tương tự phần a) ta chứng minh được O thuộc EG. Từ đó, O là giao điểm hai đường chéo của hình vuông EFGH nên O cách đều E, F, G, H.

c) BE=BC .\cot{{60}^\circ}=\frac{6\sqrt3}{3}=2\sqrt3BE=BC .cot60∘=363=23.

Đúng(0)

TT

Thạch Tít

16 tháng 10 2018 - olm

Cho hình thoi ABCD có A=60^o. Gọi E,F,G,H lần lượt là trung điểm của các cạnh AB, BC, CD, CA. Chứng minh 6 điểm E, F, G, H, B, D cùng nằm trên một đường tròn

#Toán lớp 9

0

PT

Pham Trong Bach

5 tháng 6 2019

Cho hình thoi ABCD có ∠ A = 60 ° . Gọi O là giao điểm của hai đường chéo; E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Chứng minh rằng sáu điểm E, B, F, G, D, H thuộc cùng một đường tròn.

#Toán lớp 9

1

CM

Cao Minh Tâm

5 tháng 6 2019

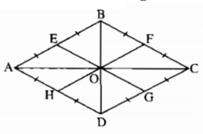
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đặt OB = OD = a. Hãy chứng minh OE = a. Tương tự, OF = OG = OH = a. Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn (O;a).

Đúng(0)

TH

Trần Hồ Tú Loan

27 tháng 9 2015 - olm

cho hình bình hành ABCD có Â=60^o,AD=2AB.Goi M la trung diem AD,N la trung diem BC.

a)CMinh tứ giác MNCD là hình thoi

b)Từ C kẻ đường thẳng vuông góc với MN tại E,cắt AB tại F. CMinh E là trung điểm CF.

c) CMinh tam giác MCF đều.

đ)CMinh F ,N ,D thẳng hàng.

#Toán lớp 8

0

PT

Pé Thỏ

28 tháng 11 2019

Cho tam giác DEF có góc D = 60$^o$ . Tính góc E và góc F biết góc E= 2. góc F

#Toán lớp 7

1

VM

Vũ Minh Tuấn

28 tháng 11 2019

Xét $\Delta DEF$ có:

$\widehat{D}+\widehat{E}+\widehat{F}=180^0$ (định lí tổng 3 góc trong một tam giác).

=> $60^0+\widehat{E}+\widehat{F}=180^0$

=> $\widehat{E}+\widehat{F}=180^0-60^0$

=> $\widehat{E}+\widehat{F}=120^0.$

Mà $\widehat{E}=2\widehat{F}\left(gt\right)$

=> $2\widehat{F}+\widehat{F}=120^0$

=> $3\widehat{F}=120^0$

=> $\widehat{F}=120^0:3$

=> $\widehat{F}=40^0.$

=> $\widehat{E}+40^0=120^0$

=> $\widehat{E}=120^0-40^0$

=> $\widehat{E}=80^0.$

Vậy $\widehat{E}=80^0;\widehat{F}=40^0.$

Chúc bạn học tốt!

Đúng(0)

S

Serein

23 tháng 7 2020 - olm

Cho hình bình hành ABCD, góc A nhọn. Kẻ DE _|_ AB tại E, DF _|_ CB tại F. AC cắt BD tại O.

a, CM : Tam giác EOF cân tại O.

b, Cho FO cắt AD tại Q. Tứ giác BQDF là hình gì? CM

c, Góc BAD = 60^o. Tính góc EOF

d, Hình bình hành ABCD có điều kiện gì để OE // AD

#Toán lớp 8

1

BB

_BQT_Smod B~ALL~F_

24 tháng 7 2020

Bạn tự vẽ hình nhé:

Mình chỉ gợi ý thôi nhé:

a, Tam giác BED vuông ở E có EO = BO = DO .

Tam giác BFD vuông ở F có: FO = OB = OD

=> EO = FO

=> Tam giác EOF cân ở O.

b, Xét tam giác QAO = tam giác FCO ( g - c - g)

=> OQ=OF

Xét tứ giác FBQD có hai đường chéo cắt nhau tại trung điểm mỗi đường nên FBQD là hình bình hành mà có góc BFD = 90 độ

=> Tứ giác FBQD là hình chữ nhật.

c, Tự chứng minh: tam giác EOB và OBF cân ở O.

Góc BAD = 60 độ => Góc ABC = 120 độ

Có góc EOF = EOB + BOF = ( 180 - 2. OBE ) + ( 180 - 2.OBF ) = 360 - 240 = 120 độ

d, Khi OE//AD => EO // BC.

Mà trong tam giác ABC có OA=OC => EA=EB

=> DE là đường trung tuyến và cũng là đường cao trong tam giác ADB.

=> Tam giác ADB cân ở D có góc BAD = 60 độ

=> Tam giác ADB đều.

=> AD = AB

=> AB = BC = CD=DA

=> Tứ giác ABCD là hình thoi.

Đúng(0)

HB

Huy Back

2 tháng 10 2017 - olm

cho hình thang cân abcd góc bac = 60, gọi o là giao điểm của hai đườg chéo gọi e, f, m lần lượt là trung điểm của ob, oc , ad.tam giác mef là hình gì

#Toán lớp 8

0

LH

Lil Học Giỏi

19 tháng 6 2019

Cho tứ giác ABCD . Â = 120^o . ∠B = 60^o . AD cắt BC tại F . AB cắt CD tại E . 2 tia phân giác của Ê và ∠F cắt nhau tại F . Chứng minh ∠EIF = 90^o .

#Toán lớp 8

1

VH

Vũ Huy Hoàng

19 tháng 6 2019

Vì là tứ giác ABCD nên khi $\widehat{A}=120^0;\widehat{B}=60^0$ thì AD//BC

Vậy ko thể nào có chuyện AD cắt BC được, trừ khi ko phải hình học phẳng

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP