Cho đồ thị hàm số C : y = 1 x ; điểm M có hoành độ x M = 2 − 3 thuộc (C). Biết tiếp tuyến của (C) tại M lần lượt cắt Ox, Oy tại A, B. Tính diện tích tam giác OAB.
A. S Δ O A B = 1.
B. S Δ O A B = 4.
C. S Δ O A B = 2.
D. S Δ O A B = 2 + 3 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’(x) ; ta thấy đồ thị hàm số y= f’(x) là parabol có trục đối xứng là trục tung nên b= 0
+ Đồ thị hàm số y= f’(x) đi qua 2 điểm (1; 5) và (0; 2) ta tìm được: a=1 và c=2.
Suy ra: f’(x) = 3x2+ 2 và f( x) = x3+ 2x+ d,
+ Do đồ thị hàm số (C) đi qua gốc toạ độ nên 0=0+0+ d
Suy ra: d= 0.
Khi đó ta có: f(x) =x3+ 2x và f( 3) –f(2) =21
Chọn D.

+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua 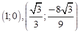 ta tìm được a=1 và b= -2
ta tìm được a=1 và b= -2
Suy ra hàm số đã cho có dạng: f(x) =x4-2x2+d và f’(x) = 4x3-4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4-2x2+1 =0 nên x=± 1
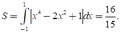
Chọn D.
Đáp án C
- Viết phương trình tiếp tuyến với C tại M.
+ Phương trình tiếp tuyến với đồ thị hàm số y = f x tại điểm M x 0 ; f x 0 :y=f ' x o x-x o +f x o .
- Tìm tọa độ hai giao điểm A,B của tiếp tuyến với các trục tọa độ Ox, Oy.
- Diện tích tam giác OAB là: S Δ O A B = 1 2 O A . O B .
y = 1 x ⇒ y ' = 1 x 2 . Ta có:
x M = 2 − 3 ⇒ y M = 1 2 − 3 = 2 + 3 ⇒ M 2- 3 ; 2 + 3 .
Phương trình tiếp tuyến với C tại M 2- 3 ; 2 + 3 là:
d : y = − y ' x M x-x M + y M = − 1 2 − 3 2 x − 2 + 3 + 2 + 3 = − 2 + 3 2 x + 4 + 2 3 .
Cho x = 0 ⇒ y = 4 + 2 3 ⇒ B 0;4+2 3
Cho
y = 0 ⇒ x = 4 + 2 3 2 + 3 = 2 2 + 3 = 4 − 2 3 ⇒ A 4 − 2 3 ; 0
Vậy S O A B = 1 2 O A . O B = 1 2 4 + 2 3 4 − 2 3 = 2 .