Hình chóp SABCD có đáy ABCD là hình chữ nhật có AD = 2a. SA = SB = a;
(SAD) ⊥ (ABCD). Tính thể tích V của hình chóp.
A. V = a 3 6 6
B. V = a 3 3 6
C. V = 2 a 3 3
D. V = a 3 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Do $SA\perp (ABCD)$ nên $\angle (SB, ABCD)=\angle (SB, AB)=\widehat{SBA}=45^0$
$\Rightarrow SAB$ là tam giác vuông cân tại $A$
$\Rightarrow SA=AB=a$
Áp dụng định lý Pitago: $SD=\sqrt{SA^2+AD^2}=\sqrt{a^2+(2a)^2}=\sqrt{5}a$

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SMA}\) là góc giữa SM và đáy
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\sqrt{3a^2+\left(\dfrac{2a}{2}\right)^2}.\sqrt{3}=2a\sqrt{3}\)
Qua B kẻ đường thẳng song song AM cắt AD kéo dài tại E
\(\Rightarrow AM||\left(SBE\right)\Rightarrow d\left(AM;SB\right)=d\left(AM;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Từ A kẻ \(AH\perp BE\) , từ A kẻ \(AK\perp SH\Rightarrow AK=d\left(A;\left(SBE\right)\right)\)
\(\widehat{DAM}=\widehat{AEB}\) (đồng vị) , mà \(\widehat{BAH}=\widehat{AEB}\) (cùng phụ \(\widehat{ABH}\))
\(\Rightarrow\widehat{DAM}=\widehat{BAH}\)
\(\Rightarrow AH=AB.cos\widehat{BAH}=AB.cos\widehat{DAM}=\dfrac{AB.AD}{AM}=\dfrac{2a.a\sqrt{3}}{2a}=a\sqrt{3}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{3a^2}+\dfrac{1}{12a^2}=\dfrac{5}{12a^2}\)
\(\Rightarrow AK=\dfrac{2a\sqrt{15}}{5}\)

Chọn gốc toạ độ tại A. Các tia Ox; Oy; Oz lần lượt trùng với các tia AD, AB, AS ta có tọa độ điểm là A(0;0;0); D(2;0;0); B ( 0 ; 2 ; 0 ) ; S ( 0 ; 0 ; 2 ) ; C 2 ; 2 ; 0 ; M 0 ; 2 2 ; 2 2 ; N 1 ; 0 ; 0
Do vậy
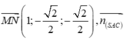
![]()
và
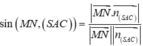
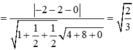
![]()
Chọn đáp án B.

Mặt phẳng (BCM) // AD nên nó cắt mặt phẳng (SAD) theo giao tuyến MN//AD
Ta có: BC ⊥ AB và BC ⊥ SA => BC ⊥ BM
Tứ giác BCNM là hình thang vuông BM là đường cao.
có : BC \(\perp\) AB và BC \(\perp\) SA \(\Rightarrow\) BC \(\perp\) BM
Tứ giác BCNM là hình thang vuông BM là đường cao
ta có : SA = AB . tan 60 = \(a\sqrt{3}\)
\(\dfrac{MN}{AD}=\dfrac{SM}{SA}\)
\(\dfrac{MN}{2a}=\dfrac{a\sqrt{3}-\dfrac{a\sqrt{3}}{3}}{a\sqrt{3}}=\dfrac{2}{3}\)
\(\Rightarrow MN=\dfrac{4a}{3}\)
\(BM=\sqrt{a^2+\dfrac{a^2}{3}}\) \(=\dfrac{2a}{\sqrt{3}}\)
diện tích hình thang BCNM là : \(S=\dfrac{2a+\dfrac{4a}{3}}{2}.\dfrac{2a}{\sqrt{3}}=\dfrac{10a^2}{3\sqrt{3}}\)
\(V_{SBCNM}=\dfrac{1}{3}.SH.S_{BCNM}\)
Hạ SH ⊥ BM
ta có : SH \(\perp\) BM
và BC \(\perp\) (SAB) \(\equiv\) (SBM) \(\Rightarrow\) BC \(\perp\) SH . vậy SH \(\perp\) (BMNC)
\(\Rightarrow\) SH là đường cao của khối chóp S.BCNM
trong \(\Delta SBA\) có \(SB=\dfrac{AB}{cos60}=2a\)
\(\Rightarrow\) \(\dfrac{AB}{SB}=\dfrac{AM}{MS}=\dfrac{1}{2}\)
BM là phân giác của góc : \(\left\{{}\begin{matrix}SBH=gt\\SBH=30^o=gt\\SH=SB.sin30^o=2a.\dfrac{1}{2}=a\end{matrix}\right.\)
\(\Leftrightarrow\) thể tích khói chóp S.BCNM là :
\(V=\dfrac{1}{3}.a.\dfrac{10a^2}{3\sqrt{3}}=\dfrac{10\sqrt{3a^2}}{27}\)

Chọn đáp án A
+ Ta có
![]()
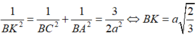
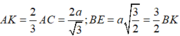
nên K là trọng tâm của tam giác BCD
+ Ta dễ dàng chứng minh được SH ⊥ (BKH) ⇒ SB, (BKH) = SBH
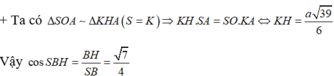
Đáp án D