cho tam giác ABC vuông tại A, biết \(\overrightarrow{AB}.\overrightarrow{CB}=4;\overrightarrow{AC}.\overrightarrow{BC}=9\) .Tìm AB,AC,BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
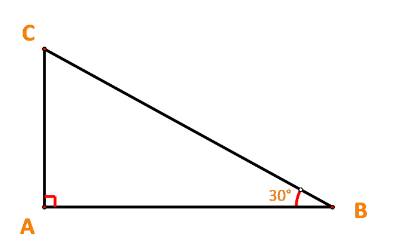
Ta có: \(BC = \frac{{AB}}{{\cos {{30}^o}}} = 3:\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \); \(AC = BC.\sin \widehat {ABC} = 2\sqrt 3 .\sin {30^o} = \sqrt 3 .\)
\(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = 3.2\sqrt 3 .\cos \widehat {ABC} = 6\sqrt 3 .\cos {30^o} = 6\sqrt 3 .\frac{{\sqrt 3 }}{2} = 9.\)
\(\overrightarrow {CA} .\overrightarrow {CB} = \left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|\cos (\overrightarrow {CA} ,\overrightarrow {CB} ) = \sqrt 3 .2\sqrt 3 .\cos \widehat {ACB} = 6.\cos {60^o} = 6.\frac{1}{2} = 3.\)
BT
12 tháng 5 2017
Dựng hình hình hành CADB.
A B C D
Theo quy tắc hình bình hành: \(\overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{CD}\).
Vì vậy \(\left|\overrightarrow{CA}+\overrightarrow{CB}\right|=\left|\overrightarrow{CD}\right|=CD\);
Mặt khác \(\left|\overrightarrow{CA}-\overrightarrow{CB}\right|=\left|\overrightarrow{CA}+\overrightarrow{BC}\right|=\left|\overrightarrow{BA}\right|=BA\).
Suy ra: \(CD=AB\).
Hình bình hành CADB có hai đường chéo bằng nhau (\(CD=AB\) )nên hình bình hành CADB là hình chữ nhật.
18 tháng 12 2022
\(\overrightarrow{CA}-\overrightarrow{CB}=\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{BA}\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
Đề thiếu, chỉ có thế này thì ko thể tính được tích vô hướng đã cho
1 tháng 10 2021
Ta có I CA+AB I = I CB I =CB
Xét tam giác ABC ( A=90 ) áp dụng định lý pytago có
CB^2 = AB^2 + AC^2 = 9+16=25 => CB=5.
Vậy I CA+AB I= I CB I =5
AH
Akai Haruma
Giáo viên
1 tháng 10 2021
Bạn lưu ý lần sau gõ lời giải bằng công thức toán (biểu tượng \(\sum\) góc trái khung soạn thảo) để được tick dễ dàng hơn khi làm đúng nhé.
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
Đặt \(AB=a\Rightarrow AC=2a\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=a\sqrt{5}\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{a^2}{a\sqrt{5}}=\dfrac{a\sqrt{5}}{5}=\dfrac{1}{5}.a\sqrt{5}\)
\(\Rightarrow BH=\dfrac{1}{5}BC\Rightarrow\overrightarrow{BH}=\dfrac{1}{5}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AH}=\overrightarrow{AB}+\overrightarrow{BH}=\overrightarrow{AB}+\dfrac{1}{5}\overrightarrow{BC}=\overrightarrow{AB}+\dfrac{1}{5}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\overrightarrow{AB}-\dfrac{1}{5}\overrightarrow{AB}+\dfrac{1}{5}\overrightarrow{AC}\)
\(=\dfrac{4}{5}\overrightarrow{AB}+\dfrac{1}{5}\overrightarrow{AC}\)
\(\Rightarrow\left\{{}\begin{matrix}m=\dfrac{4}{5}\\k=\dfrac{1}{5}\end{matrix}\right.\) \(\Rightarrow S=\dfrac{10.4}{5}+\dfrac{2020.1}{5}=412\)
Ta có \(\overrightarrow{AB}.\overrightarrow{CB}=AB.BC.cos\widehat{B}=AB.BC.\dfrac{AB}{BC}=AB^2=4\)
\(\Rightarrow AB=2\)
\(\overrightarrow{AC}.\overrightarrow{BC}=AC.BC.cos\widehat{C}=AC.BC.\dfrac{AC}{BC}=AC^2=9\)
\(\Rightarrow AC=3\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{2^2+3^2}=\sqrt{13}\)
ádhgkjhg