tìm giá trị lớn nhất M của hàm số y=a + b\(\sqrt{sinx}+c\sqrt{cosx},x\in\left[0;\frac{\pi}{4}\right],\)a2+b2+c2=3?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y=\sqrt{\left(sinx+cosx\right)^2+2\cdot sinx\cdot cosx+2}\)
\(=\sqrt{1+2sinx\cdot cosx+2\cdot sinx\cdot cosx+2}\)
\(=\sqrt{3+2sin2x}\)
\(-1< =sin2x< =1\)
=>\(-2< =2\cdot sin2x< =2\)
=>\(-2+3< =2\cdot sin2x+3< =5\)
=>\(1< =2\cdot sin2x+3< =5\)
=>\(1< =\sqrt{2\cdot sin2x+3}< =\sqrt{5}\)
=>\(1< =y< =\sqrt{5}\)
\(y_{min}=1\) khi \(sin2x=-1\)
=>\(2x=-\dfrac{\Omega}{2}+k2\Omega\)
=>\(x=-\dfrac{\Omega}{4}+k\Omega\)
\(y_{max}=\sqrt{5}\) khi sin 2x=1
=>\(2x=\dfrac{\Omega}{2}+k2\Omega\)
=>\(x=\dfrac{\Omega}{4}+k\Omega\)

Nếu miền giá trị của x có "chạm" vào \(\frac{\pi}{4}\) thì:
\(y^2=\left(a.1+b.\sqrt{sinx}+c.\sqrt{cosx}\right)^2\)
\(\Rightarrow y^2\le\left(a^2+b^2+c^2\right)\left(1+sinx+cosx\right)\)
\(\Rightarrow y^2\le3\left[1+\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\right]\le3\left(1+\sqrt{2}\right)\)
\(\Rightarrow y\le\sqrt{3+3\sqrt{2}}\)
\(M=\sqrt{3+3\sqrt{2}}\) khi \(\left\{{}\begin{matrix}x=\frac{\pi}{4}\\b=c=\sqrt{\frac{6-3\sqrt{2}}{2}}\\a=\sqrt{3\sqrt{2}-3}\end{matrix}\right.\)

a.
\(\Leftrightarrow m-cosx\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge max\left(cosx\right)\)
\(\Leftrightarrow m\ge1\)
b.
\(\Leftrightarrow2sinx-m\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\le2sinx\) ; \(\forall x\)
\(\Leftrightarrow m\le\min\limits_{x\in R}\left(2sinx\right)\)
\(\Leftrightarrow m\le-2\)
c.
\(\Leftrightarrow cosx+m\ne0\) ; \(\forall x\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\max\limits_R\left(cosx\right)\\m< \min\limits_R\left(cosx\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)

\(\Leftrightarrow\left(2m-1\right)sinx-\left(m+2\right)cosx+4m-3\ge0\) ;\(\forall x\)
\(\Leftrightarrow m\ge\dfrac{sinx+2cosx+3}{2sinx-cosx+4}=P\)
\(\Leftrightarrow m\ge P_{max}\)
Ta có: \(P=\dfrac{sinx+2cosx+3}{2sinx-cosx+4}\Leftrightarrow\left(2P-1\right)sinx-\left(P+2\right)cosx=3-4P\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(2P-1\right)^2+\left(P+2\right)^2\ge\left(3-4P\right)^2\)
\(\Leftrightarrow11P^2-24P+4\le0\)
\(\Rightarrow\dfrac{2}{11}\le P\le2\)
\(\Rightarrow m\ge2\)

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)
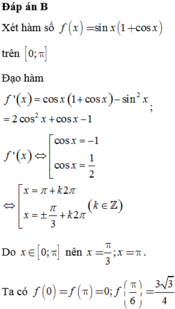
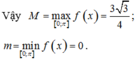
Bạn tham khảo:
Câu hỏi của Thảo Nguyễn Phương - Toán lớp 11 | Học trực tuyến