ba số x;y;z tỉ lệ nghịch với \(\dfrac{5}{2};\dfrac{4}{3};\dfrac{6}{5}\) biết \(\dfrac{x}{2}=\dfrac{z-28}{3}\)
Tìm \(B=x+y-z\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Theo giả thiết ta có: x + 2 y = 10 2 x y = 16 ⇒ y = 8 x x + 16 x = 10 ⇒ 2 y = 16 x x 2 - 10 x + 16 = 0 ⇔ [ x = 8 x = 2 2 y = 16 x
⇒ [ x = 8 2 y = 2 x = 2 2 y = 8 ⇒ x - 2 y = 6 .

Vì ba số x,y,z biết x,y,z tỉ lệ với ba số 2,3,4 nên \(\frac{x}{2} = \frac{y}{3} = \frac{z}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2} = \frac{y}{3} = \frac{z}{4} = \frac{{x - y - z}}{{2 - 3 - 4}} = \frac{2}{{ - 5}} = \frac{{ - 2}}{5}\)
Vậy \(x = 2.\frac{{ - 2}}{5} = \frac{{ - 4}}{5};y = 3.\frac{{ - 2}}{5} = \frac{{ - 6}}{5};z = 4.\frac{{ - 2}}{5} = \frac{{ - 8}}{5}\)

theo de bai ta co x phần 1 phần 5 = yphần 1/2 = zphần 1/ 4 va x^3+y^3+z^3=9512
ta còn có :
(x/1/5)^3= x^3/1/125
(y/1/2)^3= y^3/1/8
(z/1/4)^3= z^3/1/64
theo tính chất của dãy tỉ số = nhau, co:
x^3/1/125 = y^3/1/8 = z^3/1/64 = x^3+y^3+z^3 phần 1/125+1/8+1/64 = 9512 phần 1189/8000=9512*8000/1189=64000
ta có : x^3/1/125 = 64000 suy ra : x^3= 64000*1/125=512 suy ra x= 8
y^3/1/8 = 64000 suy ra : y^3= 64000*1/8 =8000 suy ra y=20
z^3/1/64 = 64000 suy ra : z^3= 64000*1/64 =1000 suy ra z=10

Chọn C.
Theo tính chất của cấp số cộng và cấp số nhân ta có
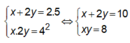
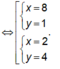
Vậy |x-2y| = 6


x=0 khi y và z là hai số đối nhau
y không thể là số 0
z=0 khi giá trị tuyệt đối của x =y2

Bài A:
Tổng 3 số bằng:
(427+688+517):2=816
Bài B:
1+2+3+...+X=500500
Tức là: (1+X) x (X:2)= 500500
<=> (1+X) x X = 500500 x 2 =1001000
Mà: 1 001 000 =1000 x 1001
Vậy X=1000
a) Gọi \(x;y;z\) lần lượt là số thứ 1;2;3
Theo đề bài ta có :
\(x+y=427\left(1\right)\)
\(y+z=688\left(2\right)\)
\(z+x=517\left(3\right)\)
\(\left(2\right)-\left(1\right)\Rightarrow z-x=261\)
\(\left(3\right)\Rightarrow z=\left(517+261\right):2=389\Rightarrow x=517-389=128\)
\(\left(2\right)\Rightarrow y=688-z=688-389=299\)
Vậy 3 số đó là \(\left\{{}\begin{matrix}x=128\\y=299\\z=389\end{matrix}\right.\)