Cho các số phân biệt \(a;\)\(b;\)\(c\)thỏa mãn \(abc\ne0\)và \(a+\frac{2}{b}=b+\frac{2}{c}=c+\frac{2}{a}\)
tính \(abc\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 12 2018
Chọn A
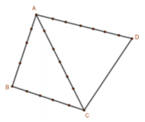
Tổng số điểm vừa lấy bằng: 3 + 4 + 5 + 6 = 18 (điểm).
Mỗi cách chọn ra 3 điểm không nằm trên một cạnh cho ta một tam giác.
Số cách chọn 3 điểm từ 18 điểm là: C 18 3 = 816(cách chọn).
Số cách chọn 3 điểm cùng nằm trên một cạnh là: 
(cách chọn).
Vậy số tam giác cần tìm bằng: 816 - 35 = 781(tam giác).
CM
11 tháng 3 2019
TH1: Tam giác được tạo thành từ 2 điểm thuộc một cạnh và điểm thứ ba thuộc một trong ba cạnh còn lại.
Có
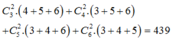
tam giác.
TH2: Tam giác được tạo thành từ ba đỉnh thuộc ba cạnh khác nhau.
Có
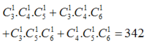
tam giác.
Vậy có 439 + 342 = 781 tam giác.
Chọn A.
DK
10 tháng 2 2017
Đáp án A
Ta có: A = 0,6; a = 0,4.
Cấu trúc di truyền của quần thế: 0,36AA : 0,48Aa : 0,16aa.
Trong số kiểu hình phân biệt được mùi vị có:
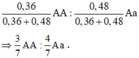
Để sinh ra một người con trai không phân biệt được mùi vị (aa) thì vợ chồng này phải có kiểu gen Aa.
Ta có P: 
.
Xác suất sinh ra người con trai không phân biệt được mùi vị: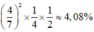 
do đó 1 sai.
Xác suất để vợ chồng này sinh ra một con trai phân biệt được mùi vị và một con gái không phân biệt được mùi vị: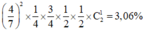 
do đó 2 đúng.
Với ý 3 ta làm như sau:
Người bố: Aa.
Người mẹ phân biệt được mùi vị có thể mang kiểu gen Aa hoặc AA.
Trường hợp 1: Người mẹ: 
.
Xác suất sinh đứa con trai mang kiểu gen dị hợp Aa là: 
Trường hợp 2: Người mẹ: 4 7 Aa
Ta có P: 
Xác suất sinh người con trai mang kiểu gen dị hợp là Aa là: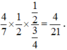 
. Vì ngay từ đầu đề bài cho bố mẹ sinh ra con có khả năng phân biệt mùi vị A-. Nên nếu con trai phân biệt mùi vị mang kiểu gen dị hợp chúng ta cần lấy tỉ lệ Aa/A-.
Vậy xác suất để sinh người con phân biệt được mùi vị là con trai và mang kiểu gen dị hợp Aa là: 
Vậy 3 sai.
Xác suất để vợ chồng này sinh 2 người con trai không phân biệt được mùi vị (aa) và 1 người con gái phân biệt được mùi vị (A-) là: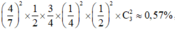 
, do đó 4 sai.
T
9 tháng 6 2021
Đáp án :
\(\Rightarrow\orbr{\begin{cases}\text{a + b + c = 6}\\\text{a + b + c = 17}\end{cases}}\)
Học tốt !!!!!!!!!!!
T
9 tháng 6 2021
Ta có :
396 = 4 x 9 x 11
Để 155a710b4c16 ⋮ 9 thì 1 + 5 + 5 + a + 7 + 1 + 0 + b = 4 + c + 16 ⋮ 9
=> 30 + a + b + c ⋮ 9 => a + b + c ∈ { 6 ; 15 ; 24 } ( do a,b,c là các chữ số )
Ta xét dấu hiệu chia hết cho 11
\(\Rightarrow\orbr{\begin{cases}\text{( 1 + 5 + 7 + 0 + 4 + 1 ) - ( 5 + a + 1 + b + c + 6 ) ⋮ 11}\\\text{( 5 + a + 1 + b + c + 6 ) - ( 1 + 5 + 7 + 0 + 4 + 1 ) ⋮ 11}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\text{18 - ( 12 + a + b + c ) ⋮ 11}\\\text{( 12 + a + b + c ) - 18 ⋮ 11}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\text{6 - a - b - c ⋮ 11}\\\text{a + b + c - 6 ⋮ 11}\end{cases}}\)
Từ 6 - a - b - c ⋮ 11 => a + b + c = 6
\(\text{Từ a + b + c - 6 ⋮ 11}\Rightarrow\orbr{\begin{cases}\text{a + b + c = 6}\\\text{a + b + c = 17}\end{cases}}\)
Vậy ................
Từ \(a+\frac{2}{b}=b+\frac{2}{c}=c+\frac{2}{a}\Rightarrow\hept{\begin{cases}a-b=\frac{2}{c}-\frac{2}{b}=\frac{2\left(b-c\right)}{bc}\\c-a=\frac{2}{b}-\frac{2}{a}=\frac{2\left(a-b\right)}{ab}\\b-c=\frac{2}{a}-\frac{2}{c}=\frac{2\left(c-a\right)}{ac}\end{cases}}\)
\(\Rightarrow\left(a-b\right)\left(c-a\right)\left(b-c\right)=\frac{8\left(a-b\right)\left(c-a\right)\left(b-c\right)}{\left(abc\right)^2}\)
\(\Leftrightarrow\frac{8}{\left(abc\right)^2}=1\Leftrightarrow8=\left(abc\right)^2\Rightarrow abc=\pm2\sqrt{2}\)