tìm tất cả giá trị m để hàm số y=\(\dfrac{mlnx-2}{lnx-m-1}\)nghịch biến trên (e\(^2\);\(+\infty\))
A. m<-2
B. m<-2 hoặc m >1
C. m<-2 hoặc m=1
D. m\(\le\)-2 hoặc m=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 3 2018
Đáp án C
Đặt t = ln x , vì x ∈ e 2 ; + ∞ ⇒ t ∈ ( 2 ; + ∞ )
Tìm m để hàm số y = m t − 2 t − m − 1 nghịch biến trên ( 2 ; + ∞ )
Ta có y ' = − m 2 − m + 2
Theo trên có y ' < 0 m + 1 ≤ 2 ⇒ − m 2 − m + 2 < 0 m ≤ 1 ⇔ m < − 2
NQ
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 1
Hàm nghịch biến trên khoảng đã cho khi:
\(-\dfrac{b}{2a}=\left|m-1\right|\le2\)
\(\Rightarrow-2\le m-1\le2\)
\(\Rightarrow-1\le m\le3\)
CM
20 tháng 6 2017
Đáp án D
Với y = ( m - 2 ) x 3 + ( m - 2 ) x 2 - x + 1 ta có y ' = 3 ( m - 2 ) x 2 + 2 ( m - 2 ) x - 1
Hàm số đã cho nghịch biến trên R
⇔ m - 2 < 0 ∆ ' ≤ 0 ⇔ m < 2 m 2 - m - 2 ≤ 0 ⇔ m < 2 - 1 ≤ m ≤ 2 ⇔ 1 ≤ m ≤ 2
CM
14 tháng 12 2019
Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
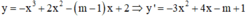
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞)
CM
26 tháng 3 2018
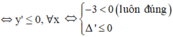
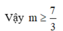
Chọn C.
y ' = 4 x 3 + 2 x 1 - m = 2 x 2 x 2 + 1 - m
Hàm số nghịch biến trên (-1; 0) nếu y ' < 0, ∀ x ∈ (-1;0)
Dễ thấy hàm số f x = 2 x 2 + 1
nên y = f (x) nghịch biến trên (-1; 0)
Vậy để m < 2x 2 + 1, ∀ x ∈ - 1 ; 0 thì m ≤ 1.
27 tháng 10 2021
a: để hàm số đồng biến trên R thì m-1>0
hay m>1
b: Để hàm số nghịch biến thì m>0
Chọn A