Giải hpt;\(\left\{{}\begin{matrix}x^3+y^3=1\\\left(x+y\right)^2y=2\end{matrix}\right.\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) m = 3 thì hệ trở thành \(\hept{\begin{cases}3x+y=3\\2x-y=7\end{cases}}\Leftrightarrow\hept{\begin{cases}6x+2y=6\left(1\right)\\6x-3y=21\left(2\right)\end{cases}}\)
\(\left(1\right)-\left(2\right)\Leftrightarrow5y=-15\Leftrightarrow y=-3\)
Từ đó suy ra \(x=2\)
Vậy với m = 3 thì hệ có 1 nghiệm (2;-3)
b) HPT không thể có nghiệm (3;1)
c) HPT có nghiệm (4;1) thì \(4m+1=3\Leftrightarrow m=\frac{1}{2}\)

a/ Xét pt : \(\left\{{}\begin{matrix}mx-y=1\\\dfrac{x}{2}-\dfrac{y}{2}=335\end{matrix}\right.\)
Khi \(m=2\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-y=1\\x-y=670\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-669\\y=-1339\end{matrix}\right.\)
b/ \(\left\{{}\begin{matrix}mx-y=1\\x-y=670\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=x-670\\mx-\left(x-670\right)=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=x-670\\x\left(m-1\right)=-669\end{matrix}\right.\)
Để pt có nghiệm duy nhất \(\Leftrightarrow m\ne1\)
Vậy...

a: \(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=6\\-5x+8y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}15x-10y=30\\-15x+24y=-9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}14x=21\\3x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-\dfrac{3}{4}\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{x}+3\sqrt{y-3}=18\\9\sqrt{x}-3\sqrt{y-3}=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=3\\\sqrt{y-3}=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=9\\y=19\end{matrix}\right.\)

Lời giải:
$y-x=2\Leftrightarrow y=x+2$
Thay vào PT $(1)$ thì:
$\frac{1}{x}+\frac{1}{x+2}=\frac{12}{35}$
$\Leftrightarrow \frac{2x+2}{x(x+2)}=\frac{12}{35}$
$\Leftrightarrow \frac{x+1}{x(x+2)}=\frac{6}{35}$
$\Rightarrow 35(x+1)=6x(x+2)$
$\Leftrightarrow 6x^2-23x-35=0$
$\Leftrightarrow (x-5)(6x+7)=0$
$\Rightarrow x=5$ hoặc $x=\frac{-7}{6}$
Với $x=5$ thì $y=x+2=2+5=7$
Với $x=\frac{-7}{6}$ thì $y=x+2=\frac{-7}{6}+2=\frac{5}{6}$

\(\Leftrightarrow\left\{{}\begin{matrix}46a+46b+14b=20,5\\a+b=0,4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}46\left(a+b\right)+14b=20,5\\a+b=0,4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}46.0,4+14b=20,5\\a+b=0,4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}14b=2,1\\a+b=0,4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=0,15\\a+0,15=0,4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=0,15\\a=0,25\end{matrix}\right.\)

Để hệ vô nghiệm thì
\(\dfrac{2m-1}{m+3}\ne\dfrac{5}{1}\\ \Leftrightarrow2m-1\ne5\left(m+3\right)\\ \Leftrightarrow m\ne-\dfrac{16}{3}\)
\(\dfrac{2m-1}{m+3}=\dfrac{3}{-4}\left(m\ne-3\right)\\ \Leftrightarrow-4\left(2m-1\right)=3\left(m+3\right)\\ \Leftrightarrow m=-\dfrac{5}{11}\left(tm\right)\)
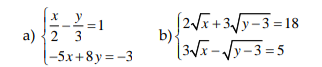
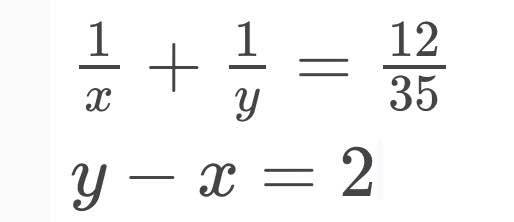


\(\Leftrightarrow\left\{{}\begin{matrix}2x^3+2y^3=2\\x^2y+2xy^2+y^3=2\end{matrix}\right.\)
\(\Rightarrow2x^3-x^2y-2xy^2+y^3=0\)
\(\Leftrightarrow\left(x-y\right)\left(2x^2+xy-y^2\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)\left(2x-y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y=x\\y=-x\\y=2x\end{matrix}\right.\) thay vào pt đầu:
\(\Rightarrow\left[{}\begin{matrix}x^3+x^3=1\\x^3+\left(-x\right)^3=1\\x^3+\left(2x\right)^3=1\end{matrix}\right.\) \(\Leftrightarrow...\)