Cho (P) có đỉnh là gốc tọa độ O và đi qua A(1;\(\frac{-1}{4}\))
Xác định đường thẳng (d) song song với đường thẳng \(y=\frac{-1}{2}x+\frac{1}{2}\)và đi qua B(0;m)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
3 tháng 6 2023
Đối xứng của A qua trục tung là A'(4; -1) và đối xứng của A qua trục hoành là A"(-4; 1).
Vậy đỉnh thứ hai của tam giác cân là I(-4; -1).
Ta có thể tính được hệ số góc của đường thẳng AI bằng công thức:
\(m=\dfrac{y_A-y_I}{x_A-x_I}=\dfrac{1-\left(-1\right)}{4-\left(-4\right)}=\dfrac{1}{4}\)
Vậy phương trình đường thẳng AI là:
\(y-y_A=m\left(x-x_A\right)\)
\(y-1=\dfrac{1}{4}\left(x-4\right)\)
\(4y-4=x-4\)
\(x-4y=0\)
Vậy phương trình đường thẳng cần tìm là \(x-4y=0\)
H
3 tháng 6 2023
Đường thẳng đi qua A và tạo với hai trục tọa độ một tam giác cân đỉnh là gốc tọa độ sẽ qua điểm trung điểm của đoạn thẳng BC, ký hiệu là M.
Có:
Tọa độ x của trung điểm M = \(\dfrac{x_B+x_C}{2}=\dfrac{3+1}{2}=2\)
Tọa độ y của trung điểm M = \(\dfrac{y_B+y_C}{2}=\dfrac{2+6}{2}=4\)
Vậy tọa độ của điểm M là (2, 4).
Phương trình đường thẳng đi qua A và M là:
\(y-1=\dfrac{4-1}{2-4}.\left(x-4\right)\Rightarrow y=-1,5x+7\)y
Vậy phương trình đường thẳng cần tìm là \(y=-1,5x+7.\)
(Cái câu kia mình làm cho bài khác tính cop màn hình mà bấm gửi nhầm ở đây, bài giải này mới đúng nhé!)
CM
10 tháng 10 2019
+ Parabol (P) đi qua A, B có hoành độ
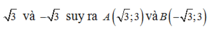
là hai điểm đối xứng nhau qua Oy.
Vậy tam giác AOB cân tại O.
+ Gọi I là giao điểm của AB và Oy suy ra ∆ IOA vuông tại I nên:
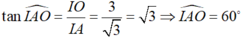
Vậy ∆AOB là tam giác đều.
Chọn B.
28 tháng 5 2018
Đồ thị biểu diễn đường đi của 1 vật bắt đầu chuyển động nhanh dần đều có dạng là
A. đường xiên góc đi qua gốc tọa độ.
B. đường parabol có đỉnh tại gốc tọa độ
C. đường thẳng xiên góc ko đi qua gốc tọa độ.
D. đường parabol ko đi qua gốc tọa độ.
CM
6 tháng 6 2018
Chọn A.
Gọi tọa độ điểm C( x ; y)
Vì O là trọng tâm tam giác ABC nên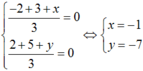 
13 tháng 7 2023
a: F(-1)=1/2(-1)^2=1/2
=>A(-1;1/2)
f(2)=1/2*2^2=2
=>B(2;2)
Theo đề, ta có hệ:
-m+n=1/2 và 2m+n=2
=>m=1/2 và n=1
b: O(0;0); A(-1;0,5); B(2;2)
\(OA=\sqrt{\left(-1-0\right)^2+0,5^2}=\dfrac{\sqrt{5}}{2}\)
\(OB=\sqrt{2^2+2^2}=2\sqrt{2}\)
\(AB=\sqrt{\left(2+1\right)^2+\left(2-0,5\right)^2}=\dfrac{3}{2}\sqrt{5}\)
\(cosO=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{-1}{\sqrt{10}}\)
=>\(sinO=\dfrac{3}{\sqrt{10}}\)
\(S_{OAB}=\dfrac{1}{2}\cdot\dfrac{\sqrt{5}}{2}\cdot2\sqrt{2}\cdot\dfrac{3}{\sqrt{10}}=\dfrac{3}{2}\)
=>\(OH=\dfrac{2\cdot\dfrac{3}{2}}{\dfrac{3}{2}\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
a) Vẽ lại hình vẽ như dưới đây
Ta có \(AB = 18,x = 3 \Rightarrow A(3;9)\)
Gọi phương trình parabol tổng quát \({y^2} = 2px\)
Thay tọa độ điểm A vào phương trình ta có: \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
Vậy phương trình parabol trên hệ trục tọa độ vừa chọn là \({y^2} = 27x\)
b) Từ câu a) ta có: \(p = \frac{{27}}{2}\)
Suy ra tiêu điểm của parabol là \(F\left( {\frac{{27}}{4};0} \right)\)
Vậy để đèn chiếu được xa phải đặt bóng đèn cách đỉnh của chóa đèn \(\frac{{27}}{4}\) xentimét
CM
19 tháng 9 2019
a) Vì A, B thuộc (P) nên:
x A = − 1 ⇒ y A = 1 2 ⋅ - 1 2 = 1 2 x B = 2 ⇒ y B = 1 2 ⋅ 2 2 = 2 ⇒ A − 1 ; 1 2 , B ( 2 ; 2 )
b) Gọi phương trình đường thẳng (d) là y = ax + b.
Ta có hệ phương trình:
− a + b = 1 2 2 a + b = 2 ⇔ 3 a = 3 2 2 a + b = 2 ⇔ a = 1 2 b = 1
Vậy (d): y = 1 2 x + 1 .
c) (d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)
=> OC = 1 và OD = 2
Gọi h là khoảng cách từ O tới (d).
Áp dụng hệ thức về cạnh và đường cao vào ∆ vuông OCD, ta có:
1 h 2 = 1 O C 2 + 1 O D 2 = 1 1 2 + 1 2 2 = 5 4 ⇒ h = 2 5 5
Vậy khoảng cách từ gốc O tới (d) là 2 5 5 .