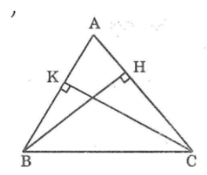
Cho tam giác ABC,có AB=AC.Kẻ BH vuông góc AC,kẻ CK vuông góc AB(H thuộc AC);(K thuoc AB) CM AH=AK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 12 2017
a) xét tam giác AHB vuông tại H và tam giác AKC vuông tại K có
góc A chung
AB = AC (gt)
Vậy tam giác AHB = tam giác AKC ( cạnh huyền góc nhọn)
suy ra BH = CK, AH = AK
b) ta có AH = AK; AB = AC
mà BK = AB - AK và HC = AC - AH
=> Bk = HC
Xét hai tam giác vuông tam giác BIK và tam giác CIH có:
góc KIB = góc HIC ( đối đỉnh)
BK = HC (cmt)
Vậy tam gics BIK = tam giác CIH
c) M là trung điểm của BC nên AM là đường trung tuyến của tam giác ABC
mà tam giác ABC là tam giác cân tại A nên AM đồng thời là trung tuyến, đường cao
mặt khác BH và Ck cũng là đường cao của tam giác ABC nên BH; CK; Am đồng quy tại 1 điểm
Suy ra A; I; M thẳng hàng
6 tháng 2 2021
Xét tam giác vuông BKC và tam giác vuông CHB có:
CK = BH (gt)
BC chung
=> Tam giác vuông BKC = Tam giác vuông CHB (ch - cgv)
=> ^B = ^C (2 góc tương ứng)
Xét tam giác ABC: ^B = ^C (cmt)
=> Tam giác ABC cân tại A
26 tháng 1 2022
Ta có: ΔABC cân tại A
=> Góc B = góc C
=> AB = AC
Xét 2 ΔKBC và ΔHCB có
Góc B = góc C
BC chung
Góc BKC = góc BHC = 90o
=> ΔKBC = ΔHCB (c - g - c)
=> BK = HC
Mà AB = AC (cmt)
=> AK = AH (dpcm)
CM
6 tháng 9 2019
Tam giác ABH vuông tại H
⇒ ∠(ABH) +∠A =90o (tính chất tam giác vuông)
⇒∠(ABH) =90o - ∠A (1)
Tam giác ACK vuông tại K
⇒∠(ACK) +∠A =90o(tính chất tam giác vuông)
⇒∠(ACK) =90o-∠A (2)
từ (1) và (2) suy ra: ∠(ACK) =∠(ABH)
9 tháng 5 2023
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
góc A chung
=>ΔABH=ΔACK
b: góc KBC+góc ICB=90 độ
góc IBC+góc HCB=90 độ
mà góc KBC=góc HCB
nên góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC
Bạn tự vẽ hình nha.
Tam giác ABC coa AB=AC=>ABC là tam giác cân tại A(ĐN)
Xét \(\Delta BCK\left(\widehat{K}=90^0\right)\) và \(\Delta CBH\left(\widehat{H}=90^0\right)\) có:
BC -chung
\(\widehat{B}=\widehat{C}\) (hai góc ở đáy của tam giác cân)
=>\(\Delta BCK=\Delta CBH\)(cạnh huyền góc nhọn) (1)
Từ (1)=>\(\widehat{HBC}=\widehat{KCB}\)mà \(\widehat{B}=\widehat{C}\) (chứng minh trên)=>Trừ vế với vế ta có :\(\widehat{ABH}=\widehat{ACK}\)
Từ (1) =>CK=BH(hai cạnh tương ứng của hai tam giác bằng nhau)
Xét \(\Delta AKC\left(\widehat{K=90^0}\right)và\Delta AHB\left(\widehat{H}=90^0\right)\) có :
\(\widehat{ABH}=\widehat{ACK}\) (chứng minh trên)
Góc A chung
=>\(\Delta AKC=\Delta AHB\)(cạnh góc vuông-góc nhọn)
=>AH=Ak(2 cạnh tương ứng của 2 tam giác bằng nhau) (ĐPCM)