Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh $\Delta$OAM = $\Delta$OCN. Từ đó suy ra tứ giác MBND là hình bình hành.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


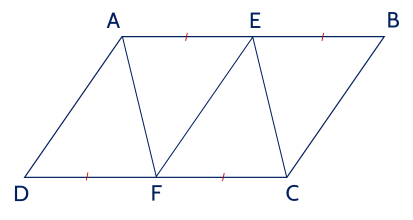
a) Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE = 1221AB, CF = DF = 1221CD
Do đó AE = BE = CF = DF.
Xét tứ giác AEFD có:
AE // DF (vì AB // CD);
AE = DF (chứng minh trên)
Do đó tứ giác AEFD là hình bình hành.
Xét tứ giác AECF có:
AE // CF (vì AB // CD);
AE = CF (chứng minh trên)
Do đó tứ giác AECF là hình bình hành.
Vậy hai tứ giác AEFD, AECF là những hình bình hành.
b) Vì tứ giác AEFD là hình bình hành nên EF = AD.
Vì tứ giác AECF là hình bình hành nên AF = EC.
Vậy EF = AD, AF = EC.

a) Ta có : t/g ABCD là hbh
Suy ra : AB//CD
Suy ra : góc FAE = góc AED ( 2 góc ở vị trí slt)
Mà góc FAE = góc DAE ( AE là tia p/g của góc A )
Suy ra : góc DAE = góc DEA
Suy ra : tam giác ADE cân tại D
b) CMTT : tam giác FBC cân tại B ( như phần a )
Suy ra : BC = BF
c) Từ (a) suy ra : AD=DE ( tam giác ADE cân tại D )
Mà BC=BF ( theo b )
Suy ra : BF=BC=AD=DE
Suy ra : DE=BF
d) Từ c) suy ra : DE=BF
Ta có : AB = AF+FB
CD=DE+CE
Mà : DE=BF ; AB=CD ( ABCD là hbh )
Suy ra : AF=CE
Xét t/g AECF có : AF//CE ( AB//CD)
AF=CE ( cmt )
Suy ra : t/g AECF là hbh.

a,
A = 20182 - 20172
A = (2018 - 2017).(2018 + 2017) = 2018 + 2017
B = (20172 - 20162)
B = (2017 - 2016).(2017 + 2016) = 2016 + 2017
Vì 2018 + 2017 > 2016 + 2017 nên A > B
b, C = 20182 + 20162; D = 2.20172
C = 20182 + 20162 - 2.20172
C - D = (20182 - 20172) - (20172 - 20162)
C - D = A - B > 0
⇒ C > D

a) Độ dài đường cao \(h\):
\(SinB=\dfrac{h}{AB}\Rightarrow h=AB.sin60^o=\dfrac{a\sqrt[]{2}}{2}\left(cm\right)\)
b) Nửa chu vi tam giác đó :
\(p=\dfrac{a+a+a}{2}=\dfrac{3a}{2}\)
Diện tích tam giác :
\(S=\sqrt[]{p\left(p-a\right)\left(p-a\right)\left(p-a\right)}\)
\(\Rightarrow S=\sqrt[]{p\left(p-a\right)^3}\)
\(\Rightarrow S=\sqrt[]{\dfrac{3a}{2}\left(\dfrac{3a}{2}-a\right)^3}=\sqrt[]{\dfrac{3a}{2}\left(\dfrac{a}{2}\right)^3}=\sqrt[]{\dfrac{3a^4}{16}}=\dfrac{a^2\sqrt[]{3}}{4}\)
a:Gọi tam giác đề bài cho là ΔABC đều có AH là đường cao
=>H là trung điểm của BC
=>HB=HC=a/2
AH=căn AB^2-AH^2
=a*căn 3/2
b: S ABC=1/2*AH*BC
=a^2*căn 3/4

Cảm ơn em câu hỏi của em thật là thù vị. Về thắc mắc của em cô nghĩ chắc cũng có nhiều bạn đang muốn biết lắm ý nhỉ? Về vấn đề em hỏi cô xin trả lời như sau:
Tình theo a ở đây không phải là a mà mình tùy chọn em nhá. a ở đây là một ẩn a, em cứ tính độ dài của tam giác đó theo ẩn a thôi em ạ!
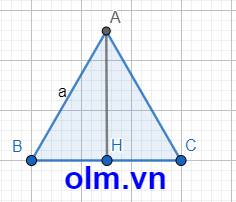
Vì ABC là tam giác đều nên đường cao cũng là đường trung tuyến của tam giác. Gọi AH là đường cao của tam giác thì
BH = HC = \(\dfrac{1}{2}\)a
Xét tam giác ACH vuông tại H. Theo pytago ta có:
AC2 = AH2 + HC2
⇒ AH2 = AC2 - HC2
⇒AH2 = a2 - (\(\dfrac{1}{2}\)a)2 = \(\dfrac{3}{4}\)a2
⇒ AH = \(\sqrt{\dfrac{3}{4}a^2}\) = \(\dfrac{3\sqrt{a}}{2}\)

Cảm ơn em đã chia sẻ bài viết rất hay và bổ ích
Cảm ơn bạn đã chia sẽ bài viết nhé. Mình sẽ áp dụng rất nhiều đó!

a, (\(x\) + y).(\(x\) + y)2 - 3\(xy\).(\(x\) + y)
= (\(x+y\))3 - 3\(x^2\)y - 3\(xy^2\)
= \(x^3\) + 3\(x^2\).y + 3\(xy^2\) + y3 - 3\(x^2\).y - 3\(xy^2\)
= \(x^3\) + y3
b, (\(x-y\)).(\(x-y\))2 - 3\(xy\).(\(x-y\))
= (\(x\) - y)3 - 3\(x^2\).y + 3\(xy^2\)
= \(x^3\) - 3\(x^2\)y + 3\(xy^2\) - y3 - 3\(x^2\)y + 3\(xy^2\)
= \(x^3\) - 6\(x^2\)y + 6\(xy^2\) - y3

Ta có:
\(2n^3+3n^2+n=n\left(2n^2+3n+1\right)\)
\(=n\left(2n^2+2n+n+1\right)\)
\(=n\left[2n\left(n+1\right)+\left(n+1\right)\right]\)
\(=n\left(n+1\right)\left(2n+1\right)\)
\(=n\left(n+1\right)\left(2n-2+3\right)\)
\(=2\left(n-1\right)n\left(n+1\right)+3n\left(n+1\right)\)
Ta có \(n-1\) ; \(n\) và \(n+1\) là \(3\) số nguyên liên tiếp
\(\Rightarrow\left(n-1\right)n\left(n+1\right)⋮2\) và \(3\)
Do đó \(\left(n-1\right)n\left(n+1\right)⋮2.3=6\)
\(\Leftrightarrow2\left(n-1\right)n\left(n+1\right)⋮6\left(1\right)\)
Ta lại có: \(n\) và \(n+1\) là 2 số nguyên liên tiếp \(\Rightarrow n\left(n+1\right)⋮2\)
Do đó: \(3n\left(n+1\right)⋮3\)
\(\Leftrightarrow3n\left(n+1\right)⋮2.3=6\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) suy ra \(2n^3+3n^2+n⋮6\)
\(2n^3-3n^2+n\left(\forall n\inℤ\right)\)
\(=n\left(2n^2-3n+1\right)\)
\(=n\left(2n^2-2n-n+1\right)\)
\(=n\left[2n\left(n-1\right)-\left(n-1\right)\right]\)
\(=n\left(n-1\right)\left(2n-1\right)\)
\(=n\left(n-1\right)\left(2n+2-3\right)\)
\(=n\left(n-1\right)\left(2n+2\right)-3n\left(n-1\right)\)
\(=2n\left(n-1\right)\left(n+1\right)-3n\left(n-1\right)\)
Ta có :
\(n\left(n-1\right)\left(n+1\right)⋮3\) (tích 3 số liên tiếp)
\(\Rightarrow2n\left(n-1\right)\left(n+1\right)⋮6\left(\forall n\inℤ\right)\left(1\right)\)
Ta lại có :
\(n\left(n-1\right)⋮2\) (tích 2 số liên tiếp là số chẵn)
\(\Rightarrow3n\left(n-1\right)⋮6\left(\forall n\inℤ\right)\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow2n\left(n-1\right)\left(n+1\right)-3n\left(n-1\right)⋮6\left(\forall n\inℤ\right)\)
\(\Rightarrow2n^3-3n^2+n⋮6\left(\forall n\inℤ\right)\)

\(2x\left(x-1\right)-\left(1-x\right)^2=0\)
\(\Leftrightarrow2x\left(x-1\right)-\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x-x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Để giải phương trình này, chúng ta có thể bắt đầu bằng cách mở ngoặc và rút gọn các thành phần. Hãy làm theo các bước sau: 1. Mở ngoặc: 2x(x-1) - (1-x)^2 = 0 => 2x^2 - 2x - (1 - 2x + x^2) = 0 2. Rút gọn các thành phần: 2x^2 - 2x - 1 + 2x - x^2 = 0 => x^2 - 1 = 0 3. Đưa phương trình về dạng chuẩn: x^2 = 1 4. Giải phương trình: - Nếu x^2 = 1, thì x có thể là 1 hoặc -1. Vậy, phương trình có hai nghiệm là x = 1 và x = -1.

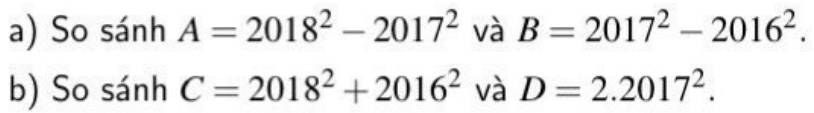

A B C D O M N
Xét tg OAM và tg OCN có
\(\widehat{BAC}=\widehat{ACD}\) (góc so le trong)
OA=OC (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
\(\widehat{AOM}=\widehat{CON}\) (góc đối đỉnh)
=> tg OAM = tg OCN (g.c.g) => AM=CN
Ta có
AB=CD (cạnh đối hbh) => AB-AM=CD-CN => MB=ND (1)
Ta có
AB//CD (cạnh đối hbh) => MB//ND (2)
Từ (1) và (2) => MBND là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
Xét tg OAM và tg OCN có
���^=���^BAC=ACD (góc so le trong)
OA=OC (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
���^=���^AOM=CON (góc đối đỉnh)
=> tg OAM = tg OCN (g.c.g) => AM=CN
Ta có
AB=CD (cạnh đối hbh) => AB-AM=CD-CN => MB=ND (1)
Ta có
AB//CD (cạnh đối hbh) => MB//ND (2)
Từ (1) và (2) => MBND là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)