1/3.4/5+1/3.6/5-4/3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(A=\dfrac{x+5}{x+1}=1+\dfrac{4}{x+1}\)
Để \(A\in Z\Rightarrow\left(x+1\right)\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
\(\Rightarrow x\in\left\{0;-2;1;-3;3;-5\right\}\)
b) \(B=\dfrac{2x+4}{x+3}=\dfrac{2\left(x+3\right)-2}{x+3}=2-\dfrac{2}{x+3}\)
Để \(B\in Z\Rightarrow\left(x+3\right)\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\Rightarrow x\in\left\{-2;-4;-1;-5\right\}\)
c) \(C=\dfrac{3x+8}{x-1}=\dfrac{3\left(x-1\right)+11}{x-1}=3+\dfrac{11}{x-1}\)
Để \(C\in Z\Rightarrow\left(x-1\right)\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
\(\Rightarrow x\in\left\{2;0;12;-10\right\}\)

\(\dfrac{1}{2014}-\dfrac{1}{2014.2013}-...-\dfrac{1}{3.2}-\dfrac{1}{2.1}\\ =\dfrac{1}{2014}-\left(\dfrac{1}{2013}-\dfrac{1}{2014}\right)-...-\left(\dfrac{1}{2}-\dfrac{1}{3}\right)-\left(1-\dfrac{1}{2}\right)\\ =\dfrac{1}{2014}+\dfrac{1}{2014}-\dfrac{1}{2013}+\dfrac{1}{2013}-\dfrac{1}{2012}+...+\dfrac{1}{3}-\dfrac{1}{2}+\dfrac{1}{2}-1\\ =\dfrac{1}{2014}+\dfrac{1}{2014}-1\\ =\dfrac{1}{1007}-1\\ =-\dfrac{1006}{1007}\)

Lấy hiệu hai phân số rồi suy ra điều phải chứng minh
\(\dfrac{-214}{317}-\dfrac{-21}{38}=\dfrac{21.317-214.38}{317.38}=\dfrac{-1475}{317.38}< 0\)
\(\Rightarrow\dfrac{-214}{317}< \dfrac{-21}{38}\)

\(\dfrac{23}{45}>\dfrac{23}{46}=\dfrac{1}{2}\)
\(\dfrac{75}{151}< \dfrac{75}{150}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{23}{45}>\dfrac{75}{151}\)


Gọi a là chiều rộng đáy của hình hộp chữ nhật.
Ta có:
\(2.60.a=2.12.a+2.12.60\Leftrightarrow120a=24a+1440\)
\(\Leftrightarrow96a=1440\Rightarrow a=15\)
Vậy chiều rộng đáy của hình hộp chữ nhật là 15 cm


Thể tích của hình lập phương cần tìm là :
8 x 4 x 2 = 64 ( dm3 )
Mà 64 dm3 = 43 dm3 nên độ dài cạnh hình lập phương đó là 4 dm
đỉnh đồi. Gió mỗi lúc mát hơn. Người đi làm rẫy chuẩn bị ra về. Sau một ngày vất vả, họ thu dọn đồ, gọi nhau cùng trở về làng bản sắc màu những bộ trang phục của họ thật đẹp trong ráng chiều.
Buổi chiều trên nương rẫy đẹp như một bức tranh thêu. Bức tranh ấy là quà tặng của thiên nhiên ban tặng cho con người. qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqwqwwwssssssssssssssssssssssssw ư qưqwqww q ………………………………………………… wwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwqqqqqqqqqqqqqqqqqqqqqqqqqqqqwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwww

\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{99.101}\\ =\dfrac{1}{2}.\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\right)\\ =\dfrac{1}{2}.\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\\ =\dfrac{1}{2}.\left(1-\dfrac{1}{101}\right)=\dfrac{1}{2}.\dfrac{100}{101}\\ =\dfrac{50}{101}\)
Đặt \(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+...+\dfrac{1}{99.101}\)
\(\Rightarrow2A=\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{99.101}\)
\(\Rightarrow2A=\dfrac{3-1}{1.3}+\dfrac{5-3}{3.5}+...+\dfrac{101-99}{99.101}\)
\(\Rightarrow2A=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\)
\(\Rightarrow2A=1-\dfrac{1}{101}=\dfrac{100}{101}\)
\(\Rightarrow A=\dfrac{50}{101}\)
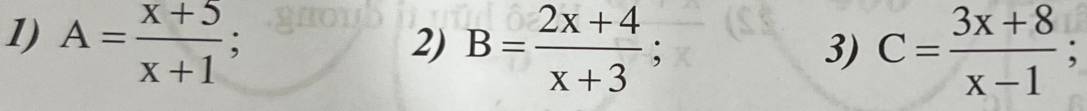

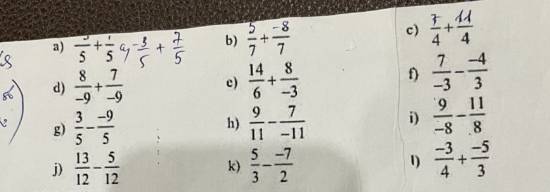
\(\dfrac{1}{3}.\dfrac{4}{5}+\dfrac{1}{3}.\dfrac{6}{5}-\dfrac{4}{3}\)
\(=\dfrac{1}{3}.\left(\dfrac{4}{5}+\dfrac{6}{5}\right)-\dfrac{4}{3}\)
\(=\dfrac{1}{3}.2-\dfrac{4}{3}\)
\(=\dfrac{2}{3}-\dfrac{4}{3}=-\dfrac{2}{3}\)
1/3 . 4/5 + 1/3 . 6/5 - 4/3
= 1/3 . ( 4/5 + 6/5 ) - 4/3
= 1/3 . 10 - 4/3
=10/3 - 4/3
=6/3