tính giá trị biểu thức P=(a^2+b^2)-(10a^2+b^2)+2(2023b+3ab),biết 3a - 2b = 2023
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: x>=-1
\(\dfrac{1}{2}\cdot\sqrt{x+1}-\dfrac{4}{3}=\sqrt{\dfrac{36}{49}}\)
=>\(\dfrac{1}{2}\cdot\sqrt{x+1}-\dfrac{4}{3}=\dfrac{6}{7}\)
=>\(\dfrac{1}{2}\cdot\sqrt{x+1}=\dfrac{4}{3}+\dfrac{6}{7}=\dfrac{28}{21}+\dfrac{18}{21}=\dfrac{46}{21}\)
=>\(\sqrt{x+1}=\dfrac{46}{21}\cdot2=\dfrac{92}{21}\)
=>\(x+1=\dfrac{8464}{441}\)
=>\(x=\dfrac{8023}{441}\)(nhận)

Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
vận tốc lúc đi là \(\dfrac{x}{4}\)(km/h)
vận tốc lúc về là \(\dfrac{x}{3}\)(km/h)
vận tốc lúc về nhanh hơn lúc đi 10km/h nên ta có:
\(\dfrac{x}{3}-\dfrac{x}{4}=10\)
=>\(\dfrac{x}{12}=10\)
=>\(x=10\cdot12=120\left(nhận\right)\)
vậy: Độ dài quãng đường AB là 120km
`#3107.101107`
Gọi quãng đường AB là x `(x < 0)`
V của người đó lúc đi: \(\dfrac{x}{4}\) (km)
V của người đó lúc về: \(\dfrac{x}{3}\) (km)
Theo đề ra, ta có phương trình:
\(\dfrac{x}{3}-\dfrac{x}{4}=10\)
\(\Rightarrow\dfrac{4x}{12}-\dfrac{3x}{12}=10\)
\(\Rightarrow\dfrac{x}{12}=10\)
\(\Rightarrow x=120\)
Vậy, quãng đường AB dài `120` km.

68,15 + (\(x\) : 8 + \(x\) x 5) = 98,9
\(x\) : 8 + \(x\) x 5 = 98,8 - 68,15
\(x\) x 0,125 + \(x\) x 5 = 30,65
\(x\) x (0,125 + 5) = 30,65
\(x\) x 5,125 = 30,65
\(x\) = 30,65 : 5,125
\(x\) = 6

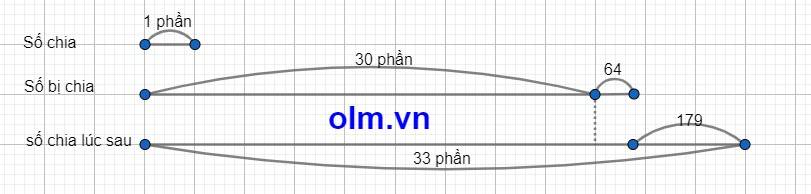
Đây là toán nâng cao chuyên đề phép chia có dư, cấu trúc thi chuyên, thi học sinh giỏi, thi violympic. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng sơ đồ đoạn thằng như sau.
Giải:
Coi số chia là một phần,
Thì số bị chia là 30 phần như thế và 64 đơn vị
Số bị chia lúc sau là 33 phần như thế
Ta có sơ đồ:
Theo sơ đồ ta có:
Số chia là: (179 + 64) : (33 - 30) = 81
Số bị chia là: 30 x 81 + 64 = 2494
Đáp số: số chia là 81
số bị chia là 2494

1: Xét tứ giác ABCK có \(\widehat{BAC}=\widehat{BKC}=90^0\)
nên ABCK là tứ giác nội tiếp
2:
Xét ΔCKB vuông tại K và ΔCEF vuông tại E có
\(\widehat{KCB}\) chung
Do đó: ΔCKB~ΔCEF
=>\(\dfrac{CK}{CE}=\dfrac{CB}{CF}\)
=>\(CK\cdot CF=CB\cdot CE\)
Xét ΔACB vuông tại A có AE là đường cao
nên \(CE\cdot CB=CA^2\)
=>\(CA^2=CK\cdot CF\)
=>\(\dfrac{CA}{CF}=\dfrac{CK}{CA}\)
Xét ΔCAK và ΔCFA có
\(\dfrac{CA}{CF}=\dfrac{CK}{CA}\)
\(\widehat{ACK}\) chung
Do đó: ΔCAK~ΔCFA
1. Chứng minh tứ giác ABCK nội tiếp:
Ta có ∆ABC vuông tại A, do đó góc ACB là góc vuông.
Gọi H là trực tâm của ∆BFC, suy ra BH ⊥ FC.
Vì A là trung điểm của EF, AE = EF và AE ⊥ BC (vì AE là đường cao), suy ra E là trung điểm của BC.
Từ đó, BK cũng là đường cao của ∆BFC, suy ra BK ⊥ FC.
Vậy tứ giác ABCK có hai đường chéo AC và BK cùng vuông góc với cạnh BC, suy ra tứ giác ABCK nội tiếp đường tròn đường kính BC.
2. Chứng minh tam giác CAK đồng dạng với tam giác CFA:
Vì tứ giác ABCK nội tiếp, suy ra góc BAC = góc BKC (cùng chắn cung BC).
Góc BAC là góc vuông (vì ∆ABC vuông tại A), suy ra góc BKC cũng là góc vuông.
Do đó, ∆BKC vuông tại K.
Vì ∆ABC vuông tại A, suy ra góc ABC + góc BAC = 90°.
Tương tự, trong ∆BFC vuông tại F, ta có góc BFC + góc FBC = 90°.
Vì E là trung điểm của BC, suy ra BE = EC và góc ABC = góc FBC.
Từ đó, góc BAC = góc BKC và góc ABC = góc FBC, suy ra ∆CAK đồng dạng với ∆CFA theo trường hợp góc-góc.
3. Chứng minh H là trung điểm của AE:
Vì H là trực tâm của ∆BFC, suy ra BH ⊥ FC và CH ⊥ BF.
Vì BK là đường cao của ∆BFC, suy ra BK ⊥ FC.
Vì E là trung điểm của BC và AE ⊥ BC, suy ra AE là đường trung bình của ∆BFC.
Đường trung bình trong tam giác vuông cũng là đường cao, suy ra H là giao điểm của AE và BK.
Do đó, H chia AE thành hai đoạn bằng nhau, suy ra H là trung điểm của AE.
\(P=\left(a^2+b^2\right)-\left(10a^2+b^2\right)+2\left(2023b+3ab\right)\)
\(=a^2+b^2-10a^2-b^2+2\left[b\left(3a-2b\right)+3ab\right]\)
\(=-9a^2+2\left(3ab-2b^2+3ab\right)\)
\(=-9a^2+12ab-4b^2\)
\(=-\left(3a-2b\right)^2=-2023^2=-4092529\)