Cho đường thẳng xy. Lấy điểm O thuộc đường thẳng xy. Trên tia Ox lấy điểm O sao cho OA = 3 cm . Trên tia Oy, lấy điểm B sao cho AB = 6 cm.
a) Kể tên các cặp tia đối nhau gốc A trên hình vẽ?
b) Tính độ dài đoạn thẳng OB.
c) Điểm O có là trung điểm của đoạn thẳng AB không? Giải thích tại sao?

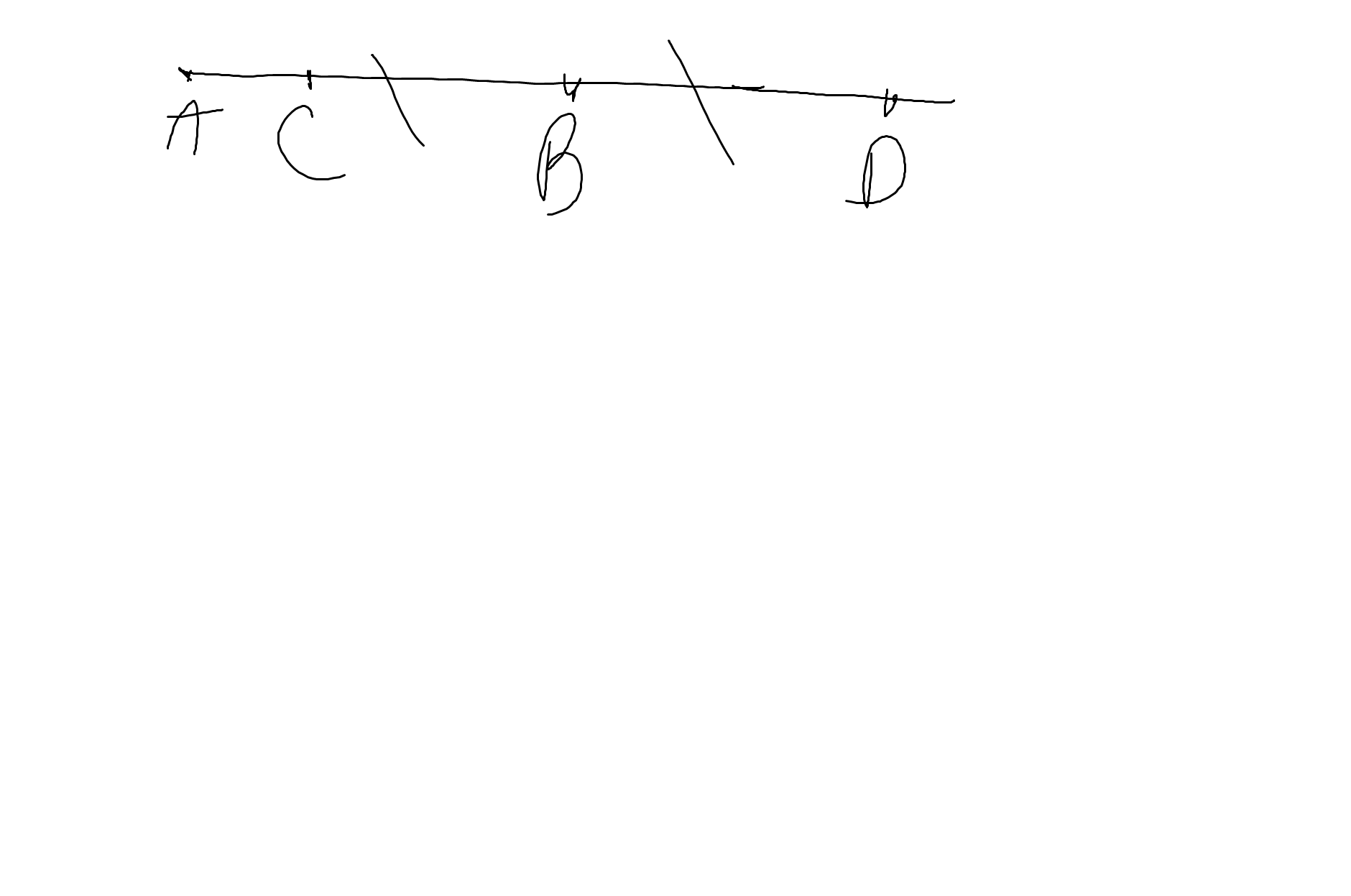
 giup mik vs
giup mik vs

a: Các cặp tia đối nhau gốc A là:
AB,Ax
AO,Ax
Ay,Ax
b: Trên tia Ay, ta có: AO<AB(3cm<6cm)
nên O nằm giữa A và B
=>AO+OB=AB
=>OB+3=6
=>OB=3(cm)
c: Vì O nằm giữa A và B
và OA=OB(=3cm)
nên O là trung điểm của AB
a) Cặp tia đối nhau gốc A trên hình vẽ là tia OA và tia AO.
b) Độ dài đoạn thẳng OB có thể tính bằng cách sử dụng định lý Pythagoras trong tam giác vuông OAB:
OB² = OA² + AB²
OB² = 3² + 6²
OB² = 9 + 36
OB² = 45
OB = √45 ≈ 6.71 cm
c) Điểm O không phải là trung điểm của đoạn thẳng AB. Để chứng minh điều này, ta có thể tính độ dài của OA và OB:
OA = 3 cm
OB = 6.71 cm
Ta thấy OA ≠ OB, do đó O không là trung điểm của AB.
tick mik nha