2 mũ 100 - 2 mũ 99 + 2 mũ 98 - 2 mũ 97...+ 2 mũ 2 _ 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(2x - 3)3 = -64
(2x - 3)3 = (-4)3
2x - 3 = -4
2x = -1
x = -1/2


Khi Trần Quốc Tuấn còn nhỏ, thân phụ ông với vua Trần Thái Tông, vốn là hai anh em trở nên bất hòa. Năm 1251, trước khi qua đời, Trần Liễu trăng trối với con trai rằng: "Con hãy vì cha mà lấy thiên hạ. Nếu không, nơi chín suối, cha không thể nhắm mắt!". Trần Quốc Tuấn tuy gật đầu, nhưng ông không cho đó là điều phải mà luôn tìm mọi cách xóa bỏ mọi hiềm khích trong hoàng tộc.
Cuối năm 1284, giặc Nguyên - Mông sắp kéo đại binh sang xâm lược nước ta, Trần Quốc Tuấn được vua Trần Nhân Tông cử làm Tiết chế thống lĩnh. Từ Vạn Kiếp, Vương kéo quân mã về Thăng Long để cùng Triều đình bàn kế chống giặc.
Một hôm, Trần Quốc Tuấn mời Thái sư Thượng tướng quân Trần Quang Khải xuống chiếc thuyền đóng tại Đông Bộ Đầu để đàm đạo. Trần Quốc Tuấn đã dùng nước thơm tắm cho Trần Quang Khải. Vừa dội nước thơm lên người Thái sư, vị Tiết chế Quốc công nói:
Thật hạnh ngộ, tôi được tắm hầu Thái sư.
Diễm phúc biết bao, tôi được Quốc công tắm cho.
Từ đó, mối tị hiềm giữa hai người được xóa bỏ hẳn.
Lúc bấy giờ thế giặc mạnh lắm, ta nên "đánh" hay nên "hòa"? Trần Quốc Tuấn đã xin Thái Thượng hoàng Trần Thánh Tông và vua Trần Nhân Tông mời các bô lão cao tuổi nhất, danh vọng nhất về Thăng Long để bàn kế giữ nước. Tại điện Diên Hồng tiếng hô "Quyết chiến! Quyết chiến!" của các bô lão rung chuyển Kinh thành.
Trần Quốc Tuấn viết "Hịch tướng sĩ" và "Binh thư yếu lược". Tướng sĩ hăm hở luyện tập cung tên, giáo mác, chiến mã. Hàng vạn hùng binh thích vào cánh tay hai chữ "Sát Thát".. Mùa hè năm 1285, 50 vạn quân xâm lược Nguyên - Mông bị đánh tơi tả. Toa Đô bị quân ta chém đầu. Thoát Hoan phải chui vào ống đồng tránh mũi tên tẩm thuốc độc mới thoát chết!
Thời bấy giờ nhà Đường ở Trung Quốc cai trị nước Việt. Từ giữa thế kỷ IX, nhà Đường phải đối phó với hai biến cố lớn là nông dân khởi nghĩa và phiên trấn cát cứ. Năm 907, nhà Đường mất, Chu Ôn lập nên nhà Hậu Lương, bắt đầu cuộc loạn Ngũ Đại, sử Trung Quốc gọi là Ngũ đại Thập quốc. Ở miền Nam Trung Quốc, Tiết độ sứ Quảng Châu là Lưu Nham đã cát cứ và dựng nước Nam Hán.[7]
Năm 905, nhân việc nhà Đường có loạn, một thổ hào người Việt là Khúc Thừa Dụ nổi lên đánh đuổi người Trung Quốc, chiếm giữ phủ thành, xưng là Tiết độ sứ. Năm 907, Khúc Thừa Dụ chết, con là Khúc Hạo lên thay. Khúc Hạo sai con là Khúc Thừa Mỹ làm Hoan hảo sứ sang dò xét nhà Nam Hán. Năm 917, Khúc Hạo chết, Khúc Thừa Mỹ lên thay, cho người sang nhà Lương lĩnh tiết việt, muốn lợi dụng sự mâu thuẫn giữa nước Lương và Nam Hán để củng cố sự nghiệp tự cường của mình. Vua Nam Hán là Lưu Cung tức giận, xua quân chiếm cứ Giao Chỉ. Năm 923, tướng Nam Hán Lý Khắc Chính đem binh đánh, bắt được Khúc Thừa Mỹ, Lý Khắc Chính lưu lại Giao Chỉ.[8]
Một hào trưởng người Ái Châu (thuộc Thanh Hóa ngày nay) là Dương Đình Nghệ nuôi 3000 con nuôi, mưu đồ khôi phục. Ngô Quyền lớn lên làm nha tướng cho Dương Đình Nghệ, được Dương Đình Nghệ gả con gái cho và giao quyền cai quản Ái châu, đất bản bộ của họ Dương. Năm 931, Dương Đình Nghệ phát binh từ Thanh Hóa ra Bắc đánh đuổi quân Nam Hán, đánh bại Lý Tiến và quân cứu viện do Trần Bảo chỉ huy, chiếm giữ bờ cõi nước Việt, xưng là Tiết độ sứ. Năm 937, hào trưởng đất Phong Châu là Kiều Công Tiễn sát hại Dương Đình Nghệ, trở thành vị Tĩnh Hải quân Tiết độ sứ cuối cùng trong thời kì Tự chủ. Nhưng Công Tiễn lại không có chỗ dựa chính trị vững chắc, hành động tranh giành quyền lực của ông bị phản đối bởi nhiều thế lực địa phương và thậm chí nội bộ họ Kiều cũng chia rẽ trầm trọng. Bị cô lập, Công Tiễn vội vã cầu cứu nhà Nam Hán. Ngô Quyền nhanh chóng tập hợp lực lượng, kéo quân ra Bắc, giết chết Kiều Công Tiễn rồi chuẩn bị quyết chiến với quân Nam Hán. Thắng lợi của Ngô Quyền trên sông Bạch Đằng vào năm 938 đã đặt dấu chấm hết cho mọi âm mưu xâm lược Tĩnh Hải quân của nhà Nam Hán, đồng thời cũng kết thúc thời kì Bắc thuộc của Việt Nam. Năm 939, Ngô Quyền xưng vương, đóng đô ở Cổ Loa, lập ra nhà Ngô. Ngô Vương qua đời ở tuổi 47, trị vì được 6 năm. Sau cái chết của ông, nhà Ngô suy yếu nhanh chóng, không khống chế được các thế lực cát cứ địa phương và sụp đổ vào năm 965.
Tháng 10/938 Ngô Quyền truy sát Kiều Công Tiễn. Kiều Công Tiễn chạy sang Trung Quốc cầu cứu quân Nam Hán. Lợi dụng cơ hội đó, Nam Hán kéo sang xâm lược Tĩnh Hải quân lần hai.
Năm 938, sau khi Kiều Công Tiễn giết Dương Đình Nghệ, Ngô Quyền được tin về việc phản nghịch của Công Tiễn và thấy việc Công Tiễn quy phục Nam Hán là nguy hại cho cuộc tự chủ mà họ Khúc và Dương Đình Nghệ cố gắng xây nền móng nên phát binh từ Ái châu ra đánh Kiều Công Tiễn. Kiều Công Tiễn sai sứ sang đút lót để cầu cứu với nhà Nam Hán. Sách An Nam chí lược viết rằng: Công Tiễn bị Ngô Quyền vây, sức yếu bị thua mới cầu cứu nhà Nam Hán.[9] Vua Nam Hán là Lưu Cung nhân Giao Chỉ có loạn muốn chiếm lấy. Lưu Cung phong cho con mình là Vạn vương Lưu Hoằng Tháo làm Giao Vương, đem quân cứu Kiều Công Tiễn. Nhưng khi quân Nam Hán chưa sang, mùa thu năm 938, Ngô Quyền đã giết được Kiều Công Tiễn.[10][11]
Lưu Cung tự làm tướng, đóng ở Hải Môn để làm thanh viện. Lưu Cung hỏi kế ở Sùng Văn sứ là Tiêu Ích, Tiêu Ích nói: "Nay mưa dầm đã mấy tuần, đường biển thì xa xôi nguy hiểm, Ngô Quyền lại là người kiệt hiệt, không thể khinh suất được. Đại quân phải nên thận trọng chắc chắn, dùng nhiều người hướng đạo rồi sau mới nên tiến".
Ngô Quyền nghe tin Hoằng Tháo sắp đến, bảo các tướng tá rằng: Hoằng Tháo là đứa trẻ khờ dại, đem quân từ xa đến, quân lính còn mỏi mệt, lại nghe Công Tiễn đã chết, không có người làm nội ứng, đã mất vía trước rồi. Quân ta lấy sức còn khỏe địch với quân mỏi mệt, tất phá được. Nhưng bọn chúng có lợi ở chiến thuyền, ta không phòng bị trước thì thế được thua chưa biết ra sao. Nếu sai người đem cọc lớn vạt nhọn đầu bịt sắt đóng ngầm ở trước cửa biển, thuyền của bọn chúng theo nước triều lên vào trong hàng cọc thì sau đó ta dễ bề chế ngự, không cho chiếc nào ra thoát.[10]
Trận bạch đằng khắc lại bằng đồng
 Tranh giả đồng tái hiện trận Bạch Đằng 938
Tranh giả đồng tái hiện trận Bạch Đằng 938
Ngô Quyền định kế rồi, bèn cho đóng cọc ở hai bên cửa biển. Khi nước triều lên, Ngô Quyền sai người đem thuyền nhẹ ra khiêu chiến, giả thua chạy để dụ quân Nam Hán đuổi theo. Hoằng Tháo quả nhiên tiến quân vào. Khi binh thuyền đã vào trong vùng cắm cọc, nước triều rút, cọc nhô lên, Ngô Quyền bèn tiến quân ra đánh, ai nấy đều liều chết chiến đấu. Quân Nam Hán không kịp sửa thuyền mà nước triều rút xuống rất gấp, thuyền đều mắc vào cọc mà lật úp, rối loạn tan vỡ, quân lính chết đuối quá nửa. Ngô Quyền thừa thắng đuổi đánh, bắt được Hoằng Tháo giết đi. Vua Nam Hán đồn trú ở cửa biển để cứu trợ nhưng không làm gì được; thương khóc, thu nhặt quân lính còn sót rút về.[10]
Sử gia Ngô Sĩ Liên nhận định trong sách Đại Việt Sử ký Toàn thư:



\(7+\dfrac{13}{4}-\dfrac{3}{5}+7.\dfrac{2}{5}-\dfrac{25}{5}-\dfrac{17}{4}+\dfrac{4}{4}\)
= \((\dfrac{13}{4}-\dfrac{17}{4}+\dfrac{4}{4})-(\dfrac{3}{5}+\dfrac{7.2}{5}-\dfrac{25}{5})+7\)
=\(\dfrac{\left(-4\right)+4}{4}-(\dfrac{-8}{5})+7\)
=\(\dfrac{0}{4}+\dfrac{8}{5}+\dfrac{7.5}{5}\)
=\(0+\dfrac{8+35}{5}\)
=\(\dfrac{43}{5}\)
Đáp số: \(\dfrac{43}{5}\)

`(1/2-1/3).6^{x}.6^{x+2}=6^{15}`
`1/6 .6^{x+x+2}=6^{15}`
`6^{2x+2}=6^{16}`
`2x+2=16`
`2x=14`
`x=7`
(1/2−1/3).6x.6x+2=615
1/6 .6^{x+x+2}=6^{15}1/6.6x+x+2=615
6^{2x+2}=6^{16}62x+2=616
2x+2=162x+2=16
2x=142x=14
x=7x=7
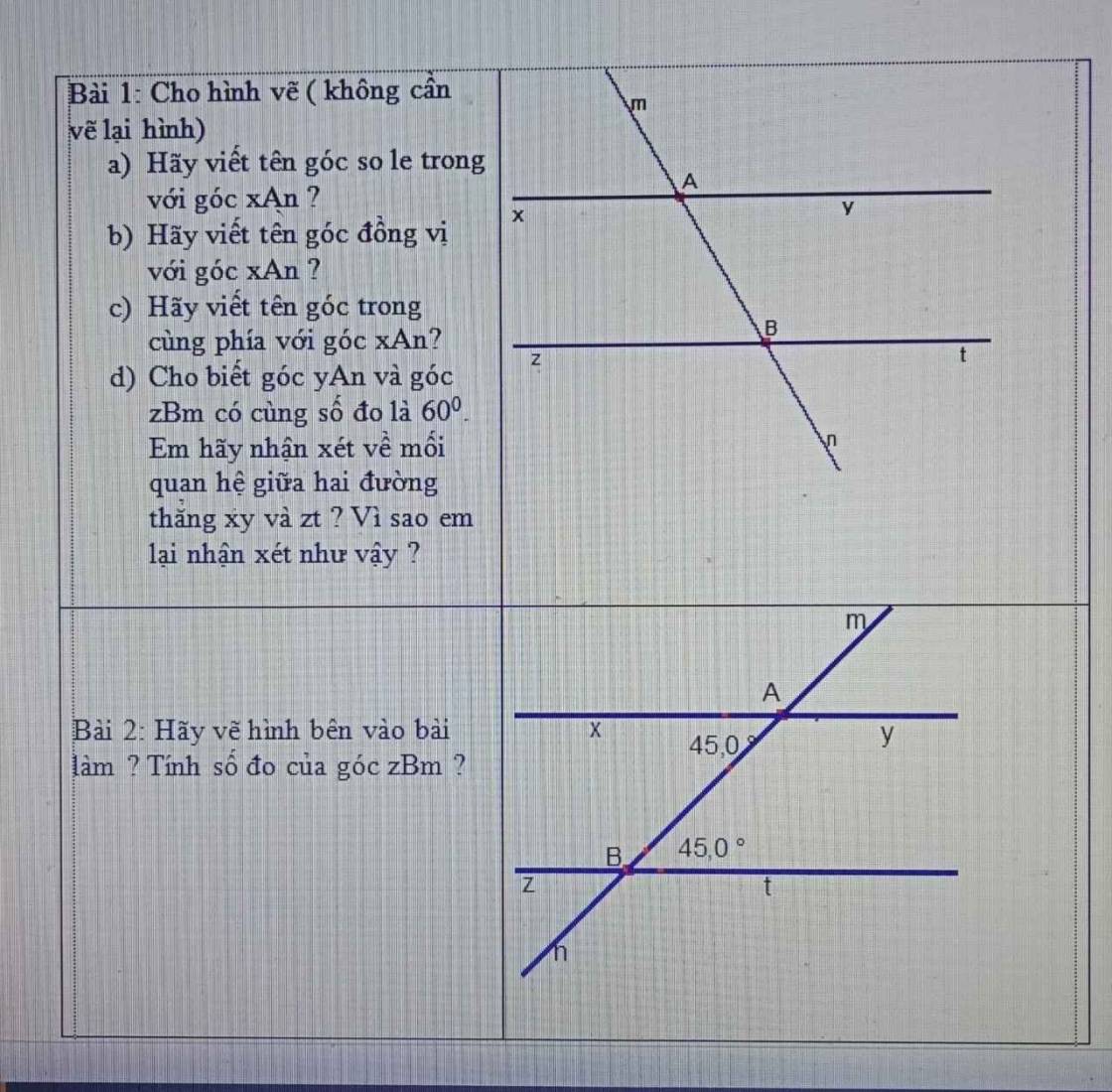
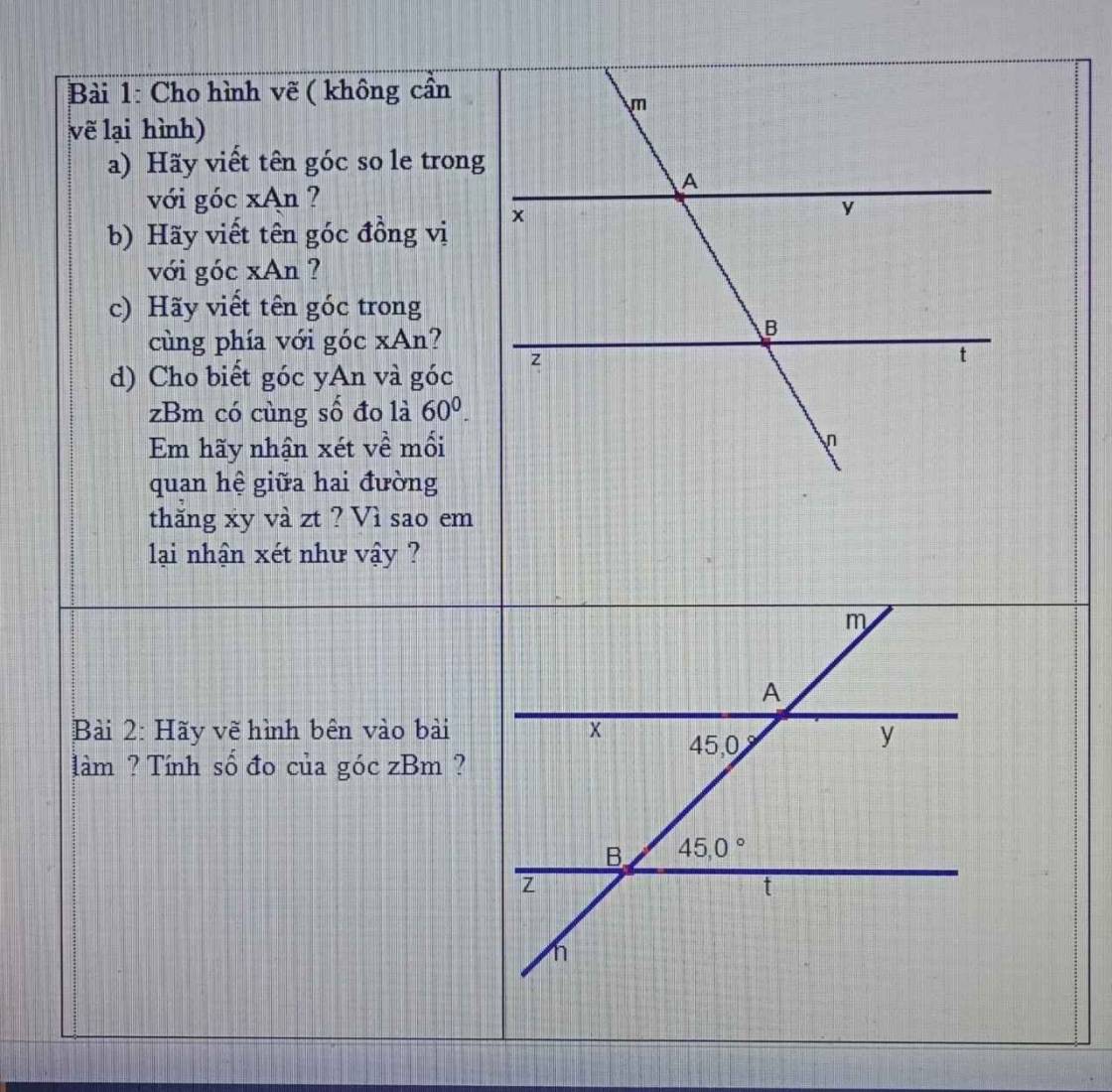
A = 2100 - 299 +298 - 297 +.....+22 -2
2.A = 2101 - 2100+299 - 298+297-........-22
2A + A= 2101 - 2
3A = 2101 - 2
A =( 2101 - 2):3