1) A= \(\dfrac{3x-y}{2x+7}\) với x-y=7, x≠ \(\dfrac{-7}{2}\), y ≠ \(\dfrac{7}{2}\)
2) B= \(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\) với \(\left\{{}\begin{matrix}x-y=9\\y\ne-3x\\x\ne3y\end{matrix}\right.\)
3)...
Đọc tiếp
1) A= \(\dfrac{3x-y}{2x+7}\) với x-y=7, x≠ \(\dfrac{-7}{2}\), y ≠ \(\dfrac{7}{2}\)
2) B= \(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\) với \(\left\{{}\begin{matrix}x-y=9\\y\ne-3x\\x\ne3y\end{matrix}\right.\)
3) C= \(\dfrac{3x^2+7y^2}{10x^2-3y^2}\) với \(\dfrac{x}{2}=\dfrac{y}{5}\) với \(10x^2\ne3y^2,y\ne0\)
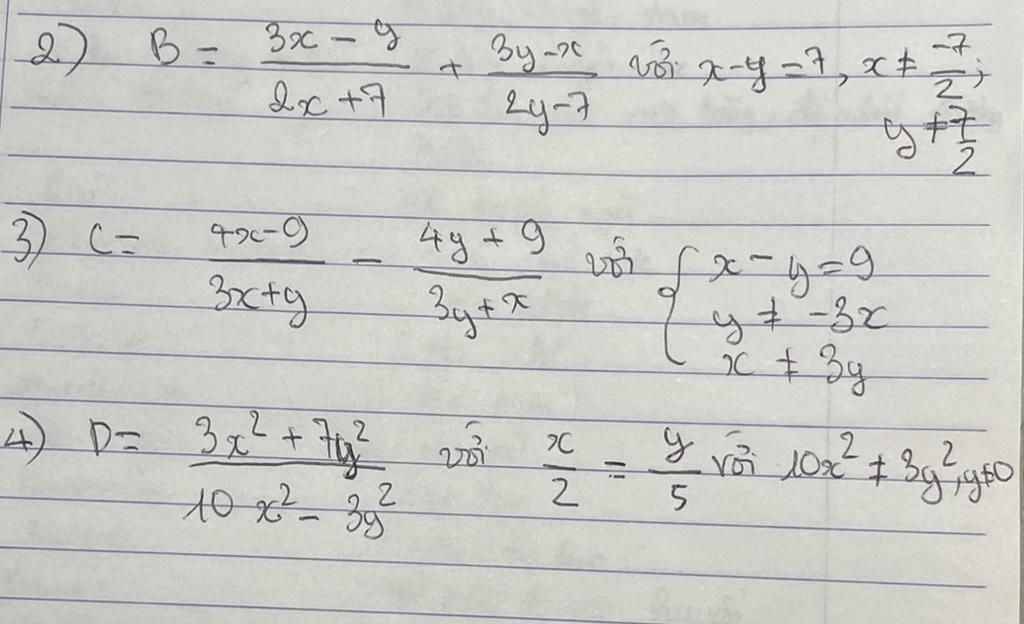
Đặt x−4=y−7=z3=kx−4=y−7=z3=k
⇒x=−4k;y=−7k;z=3k⇒x=−4k;y=−7k;z=3k(1)
Thay (1) vào ta có :
A=−2x+y+5z2x−3y−6z=−2.(−4k)+(−7k)+5.3k2.(−4k)−3.(−7k)−6.3k=8k+−7k+15k(−8k)−(−27k)−18k=k(8+−7+15)k(−8+27−18)=1617