mn ơi giúp mk với,mk cảm ơn nhiều:so sánh 202220 và 2022202210
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x+1}{3}=\dfrac{1-3x}{-5}\\ \Rightarrow-5\left(x+1\right)=3\left(1-3x\right)\\ \Rightarrow-5x-5=3-9x\\ \Leftrightarrow-5x+9x=3+5\\ \Rightarrow4x=8\\ \Rightarrow x=\dfrac{8}{4}=2\)
bạn ơi cho mình hỏi là phép tính thứ ba của bạn là ⇒−5x−5=3−9x thì tại sao bạn tính được như vậy ? Phiền bạn giúp mình nhé

Bài 1
a) \(\dfrac{2}{5}.15\dfrac{1}{3}-\dfrac{2}{5}.10\dfrac{1}{3}\)
\(=\dfrac{2}{5}.\dfrac{46}{3}-\dfrac{2}{5}.\dfrac{31}{3}\)
\(=\dfrac{2}{5}.\left(\dfrac{46}{3}-\dfrac{31}{3}\right)\)
\(=\dfrac{2}{5}.5\)
\(=2\)

\(\left(-\dfrac{1}{2}\right)^{2x-1}=-\dfrac{1}{8}\)
\(\Leftrightarrow\left(-\dfrac{1}{2}\right)^{2x-1}=\left(-\dfrac{1}{2}\right)^3\)
\(\Rightarrow2x-1=3\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\)

Ta có: \(2a=5b\Rightarrow\dfrac{a}{5}=\dfrac{b}{2}\Rightarrow\dfrac{3a}{15}=\dfrac{4b}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{3a}{15}=\dfrac{4b}{8}=\dfrac{3a+4b}{15+8}=\dfrac{46}{23}=2\)
Do đó:
\(\dfrac{a}{5}=2\Rightarrow a=5.2=10\)
\(\dfrac{b}{2}=2\Rightarrow b=2.2=4\)
Vậy a = 10, b = 4.
\(#Nulc`\)
Ta có:
\(2a=5b\Rightarrow\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{3a}{15}=\dfrac{4b}{8}=\dfrac{3a+4b}{15+8}=\dfrac{46}{23}=2\)
\(\Rightarrow\left\{{}\begin{matrix}a=5\times2=10\\b=2\times2=4\end{matrix}\right.\)

a; |2\(x\) - 4| + |3y + 21| = 0
Vì |2\(x\) - 4| ≥ 0 ∀ \(x\); |3y + 21| ≥ 0 ∀ \(x\)
vậy |2\(x\) - 4| + |3y + 21| = 0
⇔ \(\left\{{}\begin{matrix}2x-4=0\\3y+21=0\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}x=2\\y=-7\end{matrix}\right.\)
a)
\(\left|2x-4\right|+\left|3y+21\right|=0\)
Ta thấy:\(\left|2x-4\right|\ge0\forall x;\left|3y+21\right|\ge0\forall y\)
Để \(\left|2x-4\right|+\left|3y+21\right|=0\)
\(\Rightarrow\left[{}\begin{matrix}2x-4=0\\3y+21=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=4\\3y=-21\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\y=-7\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(2;-7\right)\) b) \(\left|2x-12\right|+\left|3y+9\right|=-\left|x+y+z\right|\) Vì \(\left|2x-12\right|\ge0;\left|3y+9\right|\ge0;-\left|x+y+z\right|\le0\) \(\Rightarrow\left[{}\begin{matrix}2x-12=0\\3y+9=0\\x+y+z=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=6\\y=-3\\x+y+z=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=6\\y=-3\\z=-3\end{matrix}\right.\) Vậy \(\left(x;y;z\right)=\left(6;-3;-3\right)\)
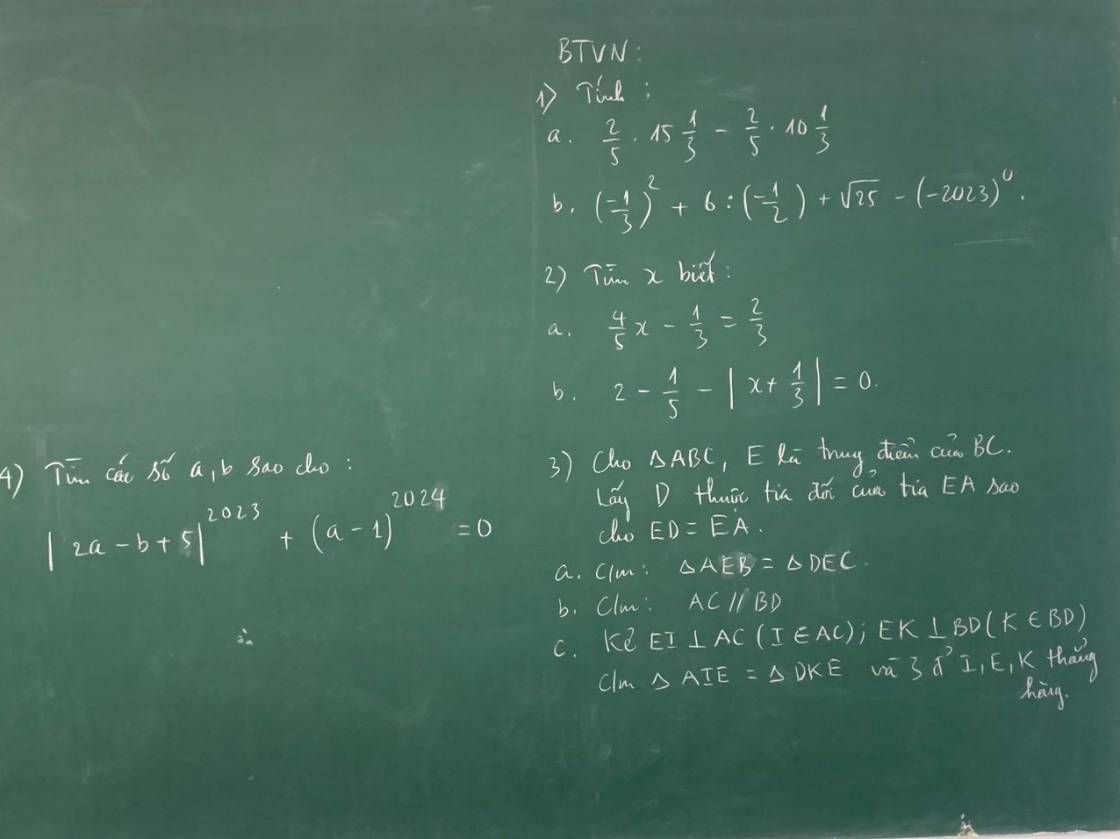


ta có 202220=(20222)10=408848410
Vì 4088484 < 20222022 nên 408848410<2022202210
Vậy 202220<2022202210
Rất dễ nhận thấy là 20222022 lớn hơn 2022 rất nhiều lần
\(\Rightarrow\)\(2022^{20}< 20222022^{10}\)