
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB~ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OA+OC}{OC}=\dfrac{OB+OD}{OD}\)
=>\(\dfrac{AC}{OC}=\dfrac{BD}{OD}\)
=>\(\dfrac{DO}{BD}=\dfrac{CO}{CA}\)
b: \(AC^2-BD^2\)
\(=AD^2+DC^2-\left(AB^2+AD^2\right)\)
\(=AD^2+DC^2-AB^2-AD^2\)
\(=DC^2-AD^2\)

a: Để (d) có hệ số góc bằng -2 thì m-1=-2
=>m=-1
b: Thay x=-3 và y=0 vào (d), ta được:
\(-3\left(m-1\right)+2m=0\)
=>-3m+3+2m=0
=>3-m=0
=>m=3
c: Thay x=0 và y=2 vào (d), ta được:
0(m-1)+2m=2
=>2m=2
=>m=1
d: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m-1=-3\\2m\ne4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=-2\\m\ne2\end{matrix}\right.\)
=>m=-2
a) Tìm để có hệ số góc bằng -2.
Hệ số góc của đường thẳng là . Để có hệ số góc bằng -2, ta giải phương trình:
b) Tìm để cắt trục hoành tại điểm có hoành độ bằng -3.
Khi cắt trục hoành, , từ đó:
c) Tìm để cắt trục tung tại điểm có tung độ bằng 2.
Khi cắt trục tung, , khi đó:
\(\Rightarrow\)
d) Tìm để song song với đường thẳng : .
Đường thẳng sẽ song song với nếu hệ số góc của bằng hệ số góc của
Kết luận:
a)
b) 3/5
c)
d)

a: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔAHB~ΔCHA
b: Ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=90^0\)
\(\widehat{BDA}+\widehat{DAH}=90^0\)(ΔDAH vuông tại H)
mà \(\widehat{CAD}=\widehat{DAH}\)
nên \(\widehat{BAD}=\widehat{BDA}\)
=>ΔBAD cân tại B
ΔBAD cân tại B
mà BF là đường phân giác
nên BF\(\perp\)AD tại F
Xét ΔEFA vuông tại F và ΔEHB vuông tại H có
\(\widehat{FEA}=\widehat{HEB}\)(hai góc đối đỉnh)
Do đó: ΔEFA~ΔEHB
=>\(\dfrac{EF}{EH}=\dfrac{EA}{EB}\)
=>\(EF\cdot EB=EA\cdot EH\)
c: Xét ΔBAK và ΔBDK có
BA=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
Do đó: ΔBAK=ΔBDK
=>\(\widehat{BAK}=\widehat{BDK}\)
=>\(\widehat{BDK}=90^0\)
=>KD\(\perp\)BC
=>KD//AH
d: Xét ΔBKD có EH//KD
nên \(\dfrac{EH}{KD}=\dfrac{BH}{BD}\)
=>\(\dfrac{EH}{KD}=\dfrac{BH}{BA}\)
Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(\dfrac{EH}{KD}=\dfrac{BA}{BC}\)
=>\(\dfrac{EH}{BA}=\dfrac{KD}{BC}\)

Lời giải:
Giả sử theo kế hoạch tổ sản xuất trong $n$ ngày.
Số sản phẩm theo kế hoạch: $50n$ (sản phẩm)
Số sản phẩm thực tế: $57(n-1)$ (sản phẩm)
Theo bài ra ta có:
$57(n-1)=50n+13$
$\Leftrightarrow 7n=70$
$\Leftrightarrow n=10$
Theo kế hoạch tổ phải sản xuất số sản phẩm là:
$50n=50.10=500$ (sản phẩm)
Gọi số sp tổ phải sản xuất theo kế hoạch là: x(sản phẩm) ĐK:x>13
\(\Rightarrow\)Thời gian dự định làm là: \(\dfrac{x}{50}\)(ngày)
Thời gian thực tế là: \(\dfrac{x+13}{57}\)(ngày)
Theo bài ra ta có pt:
\(\dfrac{x}{50}\)-\(\dfrac{x+13}{57}\)=1
\(\Leftrightarrow\)2850(\(\dfrac{x}{50}\)-\(\dfrac{x+13}{57}\))=2850
\(\Leftrightarrow\)\(57x-50x-650=2850\)
\(\Leftrightarrow\)\(7x=3500\)
\(\Leftrightarrow\)\(x=500\)
Vậy ....

- \(\dfrac{2}{5}\)\(x^2\)y.2\(xy^3\).\(\dfrac{1}{4}\)yz
= (-\(\dfrac{2}{5}\).2.\(\dfrac{1}{4}\)).(\(x^2\).\(x\)).(y.y3.y).z
= - \(\dfrac{1}{5}\)\(x^3\).y5.z
\(-\dfrac{2}{5}x^2y\cdot2xy^3\cdot\dfrac{1}{4}yz\)
\(=\left(-\dfrac{2}{5}\cdot2\cdot\dfrac{1}{4}\right)\cdot\left(x^2\cdot x\right)\cdot\left(y\cdot y^3\cdot y\right)\cdot z\)
\(=-\dfrac{1}{5}x^3y^5z\)

Lời giải:
$\frac{a+b}{c}=\frac{b+c}{a}=\frac{c+a}{b}$
$\Rightarrow \frac{a+b}{c}+1=\frac{b+c}{a}+1=\frac{c+a}{b}+1$
$\Rightarrow \frac{a+b+c}{c}=\frac{b+c+a}{a}=\frac{a+b+c}{b}$
Do $a+b+c\neq 0$ nên $c=a=b$
Khi đó:
$A=\frac{a}{b+c}+\frac{a+b}{c}+\frac{b}{c+a}=\frac{a}{a+a}+\frac{a+a}{a}+\frac{a}{a+a}=\frac{1}{2}+2+\frac{1}{2}=3$

Gọi chiều rộng khu vườn là x(m)
(Điều kiện: x>0)
Chiều dài khu vườn là x+5(m)
Chiều dài sau khi giảm 5m là x+5-5=x(m)
Chiều rộng sau khi tăng thêm 3m là x+3(m)
Diện tích giảm 10m2 nên ta có:
x(x+5)-x(x+3)=10
=>2x=10
=>x=5(nhận)
Vậy: Chiều rộng ban đầu là 5m
Chiều dài ban đầu là 5+5=10m
Gọi chiều rộng khu vườn là x(m)
(Điều kiện: x>0)
Chiều dài khu vườn là x+5(m)
Chiều dài sau khi giảm 5m là x+5-5=x(m)
Chiều rộng sau khi tăng thêm 3m là x+3(m)
Diện tích giảm 10m2 nên ta có:
x(x+5)-x(x+3)=10
=>2x=10
=>x=5(nhận)
Vậy: Chiều rộng ban đầu là 5m
Chiều dài ban đầu là 5+5=10m
Đáp số: 10 m
xin tkkkkkkkk!!!!

Gọi số ghế của mỗi dãy ban đầu là x(ghế)
(Điều kiện: \(x\in Z^+\))
Số dãy ghế ban đầu là \(\dfrac{120}{x}\left(dãy\right)\)
Số ghế ở mỗi dãy lúc sau là x+5(ghế)
Số dãy ghế lúc sau là \(\dfrac{120+72}{x+5}=\dfrac{192}{x+5}\left(dãy\right)\)
Trường phải kê thêm 3 dãy ghế nên ta có:
\(\dfrac{192}{x+5}-\dfrac{120}{x}=3\)
=>\(\dfrac{64}{x+5}-\dfrac{40}{x}=1\)
=>\(\dfrac{64x-40x-200}{x\left(x+5\right)}=1\)
=>\(x\left(x+5\right)=24x-200\)
=>\(x^2+5x-24x+200=0\)
=>\(x^2-19x+200=0\)
=>\(x\in\varnothing\)
Vậy: Không có số liệu nào thỏa mãn yêu cầu đề bài
Giải:
Gọi số ghế lúc đầu của mỗi dãy là: \(x\) (ghế); \(x\) \(\in\) N*
Số dãy ghế ban đầu là: 120 : \(x\) = \(\dfrac{120}{x}\)
Tổng số ghế lúc sau là: 120 + 72 = 192 (ghế)
Số dãy ghế lúc sau là: \(\dfrac{192}{x+5}\)
Theo bài ra ta có: \(\dfrac{192}{x+5}-\dfrac{120}{x}\) = 3
\(\dfrac{64}{x+5}-\dfrac{40}{x}=1\)
64\(x\) - 40\(x\) - 200 = .\(x\).(\(x\) + 5)
24\(x\) - 200 = \(x^2\) + 5\(x\)
\(x^2\) + 5\(x\) - 24\(x\) + 200 = 0
\(x^2\) + (5\(x-24x\)) + 200 = 0
\(x^2\) - 19\(x\) + 200 = 0
\(x^2\) - 2.\(\dfrac{19}{2}\)\(x\) + \(\dfrac{361}{4}\) + \(\dfrac{439}{4}\) = 0
(\(x-\dfrac{19}{2}\))2 + \(\dfrac{439}{4}\) = 0
(\(x-\dfrac{19}{2}\))2 ≥ 0 \(\forall\) \(x\)
⇒ (\(x-\dfrac{19}{2}\))2 + \(\dfrac{439}{2}\) ≥ \(\dfrac{439}{2}\) > 0 ∀ \(x\)
Vậy \(x\in\) \(\varnothing\)
Kết luận không có số ghế ban đầu của mỗi dãy nào thỏa mãn đề bài.


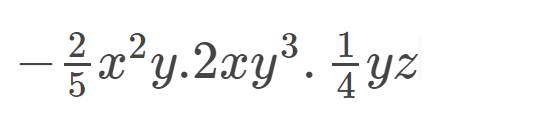
a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB~ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OA+OC}{OC}=\dfrac{OB+OD}{OD}\)
=>\(\dfrac{AC}{OC}=\dfrac{BD}{OD}\)
=>\(\dfrac{DO}{BD}=\dfrac{CO}{CA}\)
b: \(AC^2-BD^2\)
\(=AD^2+DC^2-\left(AB^2+AD^2\right)\)
\(=AD^2+DC^2-AB^2-AD^2\)
\(=DC^2-AD^2\)