(x + 1)/2022 + (x + 2)/2021 + (x + 3)/2020 = - 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A:B=11:13\)
=>\(\dfrac{A}{11}=\dfrac{B}{13}=k\)
=>A=11k; B=13k
\(\dfrac{1}{A}-\dfrac{1}{B}=\dfrac{1}{286}\)
=>\(\dfrac{1}{11k}-\dfrac{1}{13k}=\dfrac{1}{286}\)
=>\(\dfrac{13-11}{143k}=\dfrac{1}{286}\)
=>\(\dfrac{2}{143k}=\dfrac{1}{286}\)
=>\(\dfrac{2}{k}=\dfrac{1}{2}\)
=>k=4
=>\(A=11\cdot4=44;B=13\cdot4=52\)

Bài 1:
Gọi số lập được có dạng là \(\overline{abc}\)
c có 3 cách chọn
a có 6 cách chọn
b có 5 cách chọn
Do đó: Có \(3\cdot6\cdot5=90\left(số\right)\) lập được
Số số tự nhiên có 3 chữ số phân biệt lập được là \(7\cdot6\cdot5=210\left(số\right)\)
Xác suất để số được chọn là số chẵn là \(\dfrac{90}{210}=\dfrac{3}{7}\)
Bài 2:
Số cách chọn ngẫu nhiên 4 quả cầu là: \(C^4_{10}\)
Số cách chọn 4 quả cầu trắng là: \(C^4_4\)(cách)
Số cách chọn 4 quả cầu xanh là \(C^4_6\left(cách\right)\)
Xác suất để chọn được 4 quả cầu cùng màu là:
\(\dfrac{C_4^4+C_6^4}{C_{10}^4}=\dfrac{8}{105}\)

Đặt: \(n^2+3n+90=k^2\)
\(=>4n^2+12n+360=4k^2\\ =>\left(4n^2+12n+9\right)+351=4k^2\\ =>\left(2n+3\right)^2-4k^2=-351\\ =>\left(2n-2k+3\right)\left(2n+2k+3\right)=-351\)
Vì n là số tự nhiên nên: \(=>2n+2k+3>2n-2k+3\)
Ta có các trường hợp sau:
TH1: \(\left\{{}\begin{matrix}2n+2k+3=27\\2n-2k+3=-13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=2\\k=10\end{matrix}\right.\left(tm\right)\)
TH2: \(\left\{{}\begin{matrix}2n+2k+3=13\\2n-2k+3=-27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-5\\k=10\end{matrix}\right.\left(ktm\right)\)
TH3: \(\left\{{}\begin{matrix}2n+2k+3=9\\2n-2k+3=-39\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-9\\k=12\end{matrix}\right.\left(ktm\right)\)
TH4: \(\left\{{}\begin{matrix}2n+2k+3=39\\2n-2n+3=-9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=6\\k=12\end{matrix}\right.\left(tm\right)\)
TH5: \(\left\{{}\begin{matrix}2n+2k+3=3\\2n-2k+3=-117\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-30\\k=30\end{matrix}\right.\left(ktm\right)\)
TH6: \(\left\{{}\begin{matrix}2n+2k+3=117\\2n-2k+3=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=\dfrac{57}{2}\\k=\dfrac{57}{2}\end{matrix}\right.\) (ktm)
TH7: \(\left\{{}\begin{matrix}2n+2k+3=351\\2n-2k+3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=\dfrac{175}{2}\\k=88\end{matrix}\right.\left(ktm\right)\)
TH8: \(\left\{{}\begin{matrix}2n+2k+3=1\\2n-2k+3=-351\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-89\\k=88\end{matrix}\right.\)
Vậy n = 2 hoặc n = 6

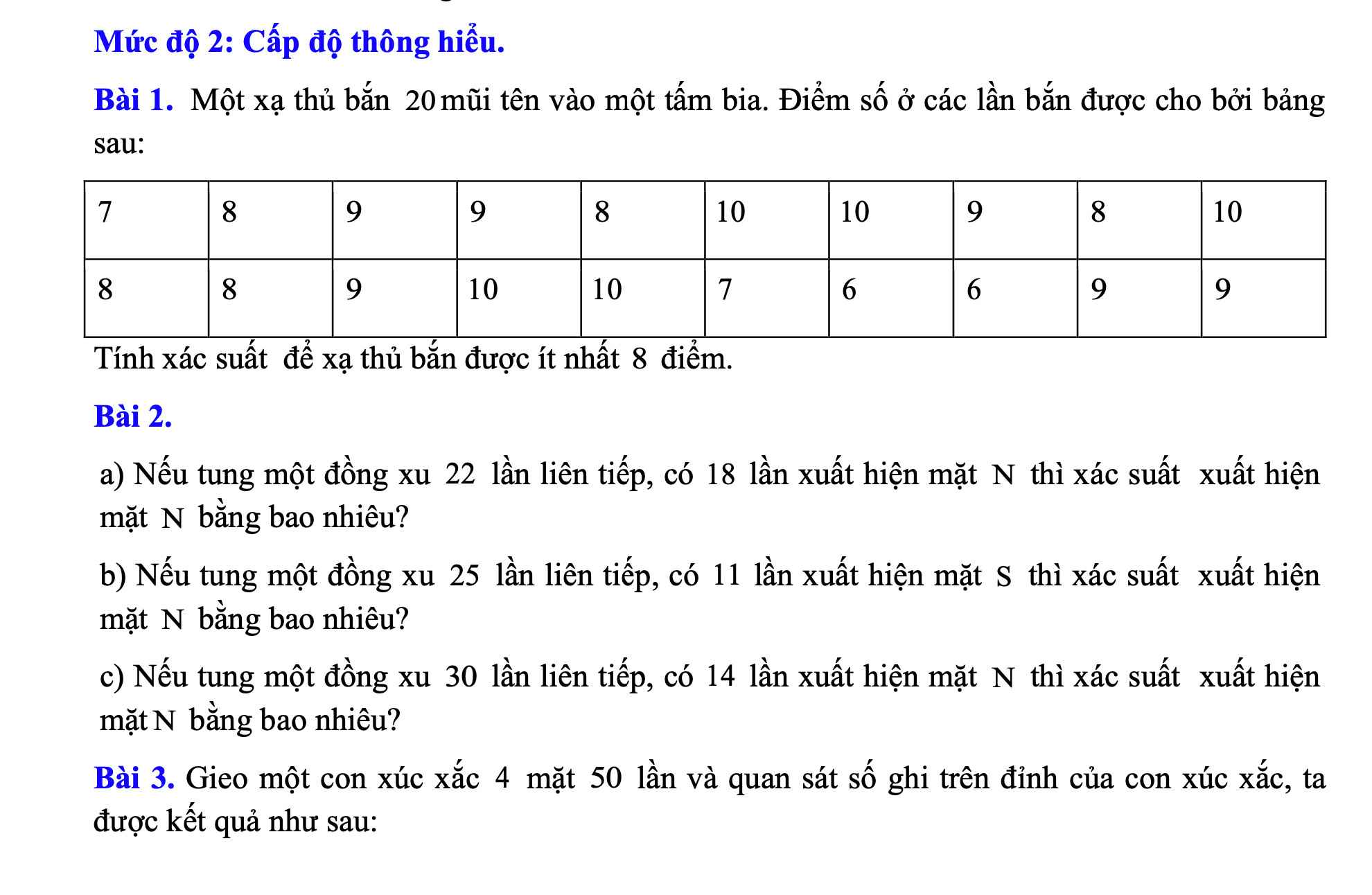
Bài 1:
Số lần bắn được ít nhất 8 điểm là:
5+6+5=16(lần)
=>Xác suất để bắn được ít nhất 8 điểm là \(P=\dfrac{16}{20}=\dfrac{4}{5}\)
Bài 2:
a: Xác suất xuất hiện mặt N là: \(\dfrac{18}{22}=\dfrac{9}{11}\)
b: Số lần xuất hiện mặt S là 25-11=14(lần)
Xác suất xuất hiện mặt S là \(\dfrac{14}{25}\)
c: Xác suất xuất hiện mặt N là \(\dfrac{14}{30}=\dfrac{7}{15}\)


Gọi x là số mét vải loại II mua được (x > 0, mét)
Số mét vải mỗi loại mua được tỉ lệ nghịch với giá tiền một mét vải là :
60/x = 120/100
Nên x = 50
Vậy số mét vải loại II mua được là 50 m

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=\dfrac{\left(bd\right)\cdot k^2}{bd}=k^2\left(1\right)\)
\(VP=\dfrac{2009a^2+2010c^2}{2009b^2+2010d^2}=\dfrac{2009\cdot\left(bk\right)^2+2010\cdot\left(dk\right)^2}{2009b^2+2010d^2}\\ =\dfrac{2009b^2\cdot k^2+2010d^2\cdot k^2}{2009b^2+2010d^2}=\dfrac{k^2\cdot\left(2009b^2+2010d^2\right)}{2009b^2+2010d^2}\\ =k^2\left(2\right)\)
Từ (1) và (2) => \(\dfrac{ac}{bd}=\dfrac{2009a^2+2010c^2}{2009b^2+2010d^2}\)

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{a^2+ac}{c^2-ac}=\dfrac{\left(bk^2\right)+bk\cdot dk}{\left(dk\right)^2-bk\cdot dk}\\ =\dfrac{b^2k^2+bdk^2}{d^2k^2-bdk^2}=\dfrac{k^2\left(b^2+bd\right)}{k^2\left(d^2-bd\right)}=\dfrac{b^2+bd}{d^2+bd}=VP\)

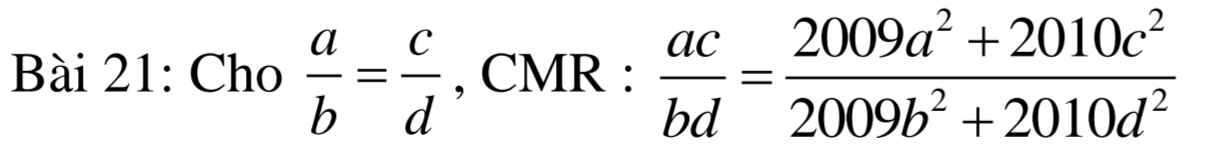
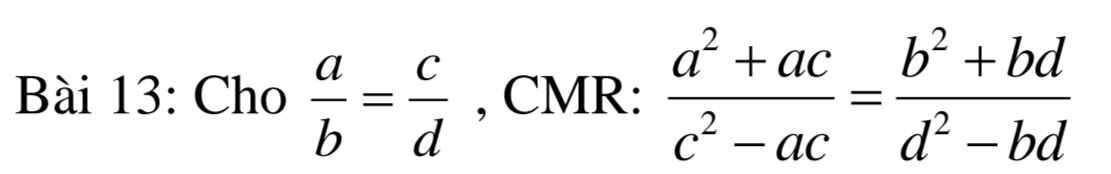
\(\dfrac{x+1}{2022}+\dfrac{x+2}{2021}+\dfrac{x+3}{2020}=-3\\ \Rightarrow\dfrac{x+1}{2022}+\dfrac{x+2}{2021}+\dfrac{x+3}{2020}+3=0\\ \left(\dfrac{x+1}{2022}+1\right)+\left(\dfrac{x+2}{2021}+1\right)+\left(\dfrac{x+3}{2020}+1\right)=0\\ \dfrac{x+2023}{2022}+\dfrac{x+2023}{2021}+\dfrac{x+2023}{2021}=0\\ \left(x+2023\right)\cdot\left(\dfrac{1}{2022}+\dfrac{1}{2021}+\dfrac{1}{2020}\right)=0\)
Vì \(\left(\dfrac{1}{2022}+\dfrac{1}{2021}+\dfrac{1}{2020}\right)\ne0\) nên:
\(x+2023=0\\ \Rightarrow x=-2023\)
Vậy \(x=-2023\)