\(s\left(t\right)=t^2-4t+3\)

=>\(v\left(t\right)=s'\left(t\right)=2t-4\)

=>\(a\left(t\right)=v'\left(t\right)=2\cdot1=2\)

=>a(4)=2

Bài 5:

a: \(A=\dfrac{1}{1\times2}+\dfrac{1}{2\times3}+...+\dfrac{1}{99\times100}\)

\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)

\(=1-\dfrac{1}{100}=\dfrac{99}{100}\)

b: \(B=\dfrac{1}{1\times3}+\dfrac{2}{3\times7}+\dfrac{1}{7\times9}+\dfrac{3}{9\times15}+\dfrac{6}{15\times27}\)

\(=\dfrac{1}{2}\left(\dfrac{2}{1\times3}+\dfrac{4}{3\times7}+\dfrac{2}{7\times9}+\dfrac{6}{9\times15}+\dfrac{12}{15\times27}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{15}+\dfrac{1}{15}-\dfrac{1}{27}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{27}\right)=\dfrac{1}{2}\times\dfrac{26}{27}=\dfrac{13}{27}\)

c: \(C=\dfrac{1}{1\times3}+\dfrac{1}{3\times5}+...+\dfrac{1}{2011\times2013}\)

\(=\dfrac{1}{2}\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+...+\dfrac{2}{2011\times2013}\right)\)

\(=\dfrac{1}{2}\times\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2011}-\dfrac{1}{2013}\right)\)

\(=\dfrac{1}{2}\times\left(1-\dfrac{1}{2013}\right)=\dfrac{1}{2}\times\dfrac{2012}{2013}=\dfrac{1006}{2013}\)

Bài 3:

a: Khi m=2006; n=2007; p=2008 thì

\(S=2006\times2+2007\times2+2008\times2=2\times\left(2006+2007+2008\right)=12042\)

b: \(S=m\times2+n\times2+p\times2=2\times\left(m+n+p\right)=2\times2009=4018\)

\(M=\dfrac{1}{1\cdot5}+\dfrac{1}{5\cdot9}+...+\dfrac{1}{n\left(n+4\right)}\)

\(=\dfrac{1}{4}\left(\dfrac{4}{1\cdot5}+\dfrac{4}{5\cdot9}+...+\dfrac{4}{n\left(n+4\right)}\right)\)

\(=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{n}-\dfrac{1}{n+4}\right)\)

\(=\dfrac{1}{4}\left(1-\dfrac{1}{n+4}\right)=\dfrac{1}{4}\cdot\dfrac{n+4-1}{n+4}=\dfrac{n+3}{4\left(n+4\right)}\)

\(\dfrac{2}{3}\) + \(x+\dfrac{1}{4}\)\(x\) = - \(\dfrac{22}{27}\)

       \(x+\dfrac{1}{4}x\) = - \(\dfrac{22}{27}\) - \(\dfrac{2}{3}\)

        \(\dfrac{5}{4}x\)      = - \(\dfrac{40}{27}\)

            \(x=-\dfrac{40}{27}:\dfrac{5}{4}\)

            \(x=-\dfrac{32}{27}\)

Vậy \(x=-\dfrac{32}{27}\)

a: Đặt a/b=c/d=k

=>\(a=bk;c=dk\)

\(\left(\dfrac{a-b}{c-d}\right)^2=\left(\dfrac{bk-b}{dk-d}\right)^2=\left(\dfrac{b\left(k-1\right)}{d\left(k-1\right)}\right)^2=\left(\dfrac{b}{d}\right)^2\)

\(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot k}=\dfrac{b^2\cdot k}{d^2\cdot k}=\dfrac{b^2}{d^2}\)

Do đó: \(\left(\dfrac{a-b}{c-d}\right)^2=\dfrac{ab}{cd}\)

b: \(\left(\dfrac{a+b}{c+d}\right)^3=\left(\dfrac{bk+b}{dk+d}\right)^3=\left(\dfrac{b\left(k+1\right)}{d\left(k+1\right)}\right)^3=\left(\dfrac{b}{d}\right)^3\)

\(\dfrac{a^3-b^3}{c^3-d^3}=\dfrac{b^3k^3-b^3}{d^3k^3-d^3}=\dfrac{b^3\left(k^3-1\right)}{d^3\left(k^3-1\right)}=\dfrac{b^3}{d^3}\)

Do đó: \(\left(\dfrac{a+b}{c+d}\right)^3=\dfrac{a^3-b^3}{c^3-d^3}\)

Trên tia ssoois của MA lấy D sao cho DM=AM

Mà BM=CM (gt)

=> ABCD là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

Ta có \(\widehat{A}=90^o\)

=> ABCD là hình chữ nhật => AD=BC (trong HCN hai đường chéo bằng nhau)

Ta có

\(AM=\dfrac{AD}{2}\) mà \(AD=BC\left(cmt\right)\Rightarrow AM=\dfrac{BC}{2}\) 

Gọi tam giác vuông đề bài cho là ΔABC vuông tại A, đường trung tuyến AM

Trên tia đối của tia MA, lấy D sao cho MA=MD

Xét ΔMAB và ΔMDC có

MA=MD

\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)

MB=MC

Do đó: ΔMAB=ΔMDC

=>\(\widehat{MAB}=\widehat{MDC}\)

=>AB//DC

Ta có: AB//DC

AB\(\perp\)AC

Do đó: CD\(\perp\)CA

Xét ΔBAC vuông tại A và ΔDCA vuông tại C có

BA=DC

AC chung

Do đó: ΔBAC=ΔDCA

=>BC=DA

mà DA=2AM

nên BC=2AM

=>\(AM=\dfrac{1}{2}BC\)(ĐPCM)

Đặt A = 2 + 2² + 2³ + ... + 2²⁰

2A = 2² + 2³ + 2⁴ + ... + 2²¹

A = 2A - A

= (2² + 2³ + 2⁴ + ... + 2²¹) - (2 + 2² + 2² + ... + 2²⁰)

= 2²¹ - 2

= 2097150

   A = 2 + 2² + 2³ + ... + 2²⁰

2.A =2.(2 + 2² + 2³ + ... + 2²⁰)

2A = 2² + 2³ + 2⁴ + ... + 2²¹

2A - A = 2² + 2³ + 2⁴ + ... + 2²¹ - (2 + 2² + 2³ + ... + 2²⁰)

A = 2² + 2³ + 2⁴ + ... + 2²¹ - 2 - 2² - ... - 2²⁰

A = (2² - 2²) + (2³ - 2³) + ... + (2²¹ - 2)

A = 0 + 0 + ... + 0 + 2²¹ - 2

A = 2²¹ - 2

      Giải:

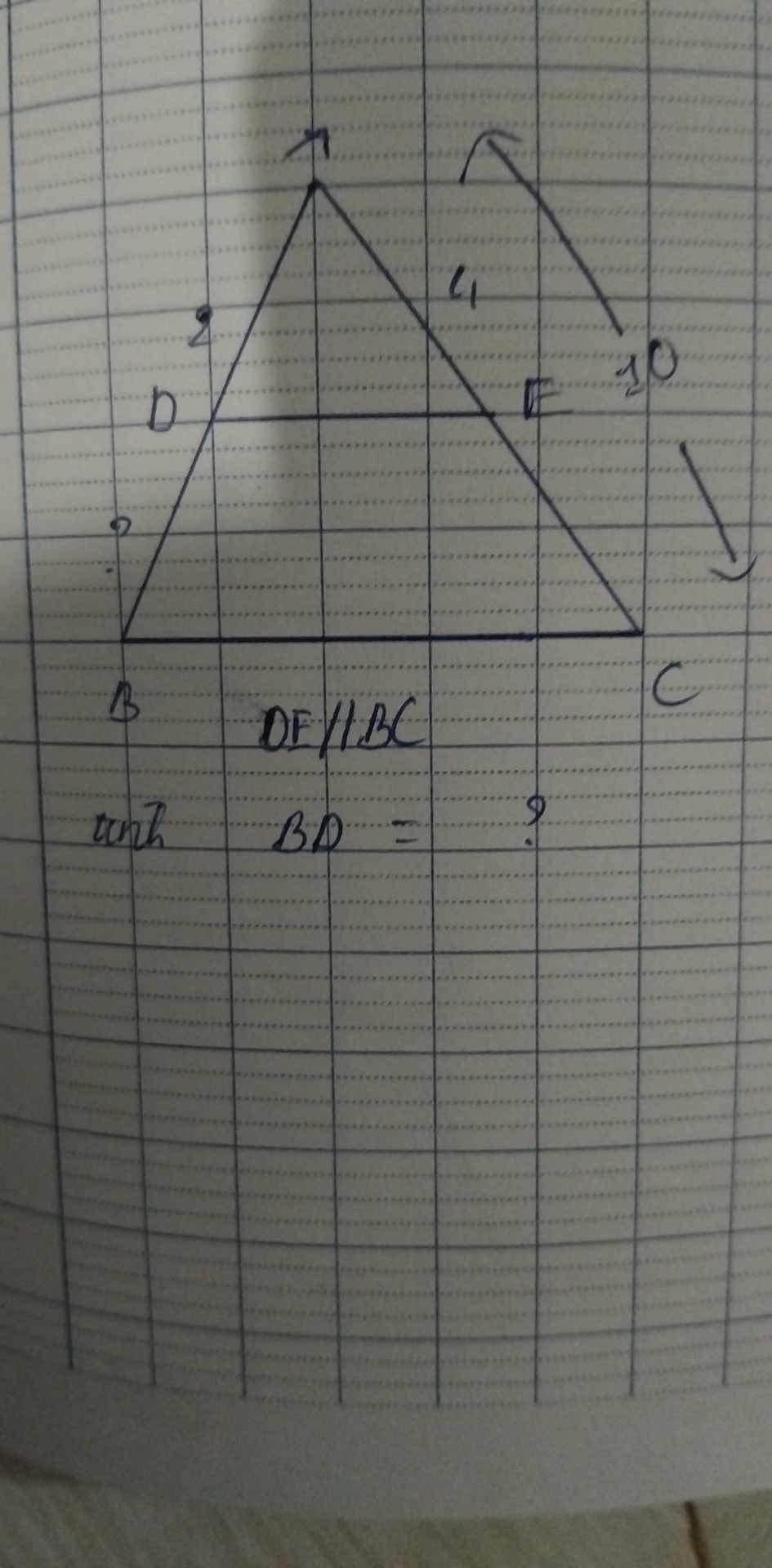
Vì DE // BC  

   \(\dfrac{AD}{AB}\) = \(\dfrac{AE}{AC}\)  (hệ quả Thalet)

⇒ \(\dfrac{2}{AB}\) = \(\dfrac{4}{10}\)

    AB = 2 : \(\dfrac{4}{10}\) 

   AB = 5 

Vậy AB =  5 cm

AB = AD + BD 

BD = AB - AD 

BD = 5 -  2 = 3

Vậy BD = 3cm

Kết luận: BD =  3cm

Ta có:

EC = AC - AE = 10 - 4 = 6

∆ABC có:

DE // BC (gt)

⇒ AD/BD = AE/EC (định lý Thales)

⇒ 2/BD = 4/6

⇒ BD = 2 . 6 : 4 = 3

Lời giải:

Gọi giá ban đầu của 1 hộp sữa là $a$ và giá 1 gói đường là $b$ (đồng)

Theo bài ra ta có:

\(\left\{\begin{matrix}\\ 9a+3b=147000\\ 9(a-1500)+3b.0,9=147000-21000\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}\\ 9a+3b=147000\\ 9a+2,7b=139500\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}\\ a=8000\\ b=25000\end{matrix}\right.\)

Diện tích mảnh vườn là:

\(1200000:20000=60\left(m^2\right)\)

Gọi chiều rộng mảnh vườn là x (m) với x>0

Chiều dài mảnh vườn là: \(x+4\) (m)

Diện tích mảnh vườn là: \(x\left(x+4\right)\) \(\left(m^2\right)\)

Do diện tích mảnh vườn là 60 \(m^2\) nên ta có pt:

\(x\left(x+4\right)=60\)

\(\Leftrightarrow x^2+4x-60=0\Rightarrow\left[{}\begin{matrix}x=6\\x=-10\left(loại\right)\end{matrix}\right.\)

Vậy mảnh vườn rộng 6m

Giải nhanh giúp mình với