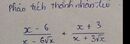Cho đường tròn (O), kẻ tiếp tuyến từ điểm P nằm ngoài đường tròn (O), kẻ 2 tiếp tuyến PA và PB. Đường thẳng kẻ từ B song song với PA cắt đường tròn (O) tại C. CP cắt đường tròn (O) tại E, BE cắt đường tròn (O) tại M. a) Chứng mình: PM^2=BM.ME b)Chứng minh M là trung điểm PA giúp mình với hicc

cp cắt (o) tại e tức e thuộc (O) rồi xong lại be cắt (o) tại m ??

Áp dụng định lí Pytago tam giác DHF vuông tại H 

\(DF=\sqrt{FH^2+DF^2}=\sqrt{9+9}=\sqrt{18}=3\sqrt{2}\)cm 

Xét tam giác ABC vuông tại A, đường cao AH

* Áp dụng hệ thức : \(DH^2=FH.HE\Rightarrow HF=\frac{DH^2}{HE}=\frac{9}{3}=3\)cm 

-> FE = 2FH = 6 cm 

Theo định lí Pytago tam giác DÈF vuông tại D

\(DE=\sqrt{FE^2-DF^2}=\sqrt{36-18}=\sqrt{18}=3\sqrt{2}\)cm 

ko cs hình ak bn

\(\frac{1-2sin^2x}{cosx-sinx}=\frac{sin^2x+cos^2x-2sin^2x}{cosx-sinx}\)

\(=\frac{cos^2x-sin^2x}{cosx-sinx}=\frac{\left(cosx+sinx\right)\left(cosx-sinx\right)}{cosx-sinx}=cosx+sinx\)

\(\frac{1-\sin^2x-\sin^2x}{\cos x-\sin x}=\frac{\cos^2x-\sin^2x}{\cos x-\sin x}=\frac{\left(\cos x-\sin x\right)\left(\cos x+\sin x\right)}{\cos x-\sin x}\cos=\cos x+\sin x\)

a.\(P=\left(\frac{\left(\sqrt{x}-1\right)^2-\left(\sqrt{x}+1\right)^2}{x-1}\right).\left(\frac{1-x}{2\sqrt{x}}\right)^2=\left(-\frac{4\sqrt{x}}{x-1}\right).\frac{\left(1-x\right)^2}{4x}=\frac{1-x}{\sqrt{x}}\)

b.P không có giá trị lớn nhất hay nhỏ nhất.

c.\(P=\frac{1-x}{\sqrt{x}}=2\Leftrightarrow x+2\sqrt{x}-1=0\Leftrightarrow\left(\sqrt{x}+1\right)^2=2\Leftrightarrow\sqrt{x}+1=\sqrt{2}\)

hay \(x=3-2\sqrt{2}\)

d.\(x=3-2\sqrt{2}\Rightarrow P=2\) (dựa vào câu c)

e.\(P>0\Leftrightarrow\hept{\begin{cases}1-x>0\\x>0\end{cases}\Leftrightarrow0< x< 1}\)

g.ta có \(P+2\sqrt{x}=\frac{1-x}{\sqrt{x}}+2\sqrt{x}=\frac{1+x}{\sqrt{x}}>0\)

Vậy \(P>-2\sqrt{x}\)