
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 6:
a: \(P=\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2+5\sqrt{x}}{x-4}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{5\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)+\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x-2\sqrt{x}+x+3\sqrt{x}+2-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2x-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\sqrt{x}}{\sqrt{x}+2}\)
b: P>1
=>P-1>0
=>\(\dfrac{2\sqrt{x}-\sqrt{x}-2}{\sqrt{x}+2}>0\)
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}>0\)
=>\(\sqrt{x}-2>0\)
=>x>4
Câu 9:
a: Xét tứ giác CEHF có \(\widehat{CEH}+\widehat{CFH}=90^0+90^0=180^0\)
nên CEHF là tứ giác nội tiếp
b: Xét ΔABC có
BF,AE là các đường cao
BF cắt AE tại H
Do đó: H là trực tâm của ΔABC
=>CH\(\perp\)AB
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD\(\perp\)BA
mà CH\(\perp\)BA
nên CH//BD
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD
mà BH\(\perp\)AC
nên BH//CD
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành

Bài 3
2b) ∆' = m² - 1.(2m - 1)
= m² - 2m + 1
= (m - 1)² > 0 với mọi m 1
Để phương trình có hai nghiệm phân biệt thỏa mãn x₁ ≤ 0 < x₂ thì:
x₁x₂ ≤ 0
⇔ 2m - 1 ≤ 0
⇔ 2m ≤ 1
⇔ m ≤ 1/2 (nhận)
Vậy m ≤ 1/2 thì phương trình có hai nghiệm thỏa mãn yêu cầu đề bài

ĐKXĐ: \(\left[{}\begin{matrix}x>=2\\x< =-2\end{matrix}\right.\)
\(\dfrac{1}{4}\sqrt{x^2-4}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{1}{4}\sqrt{x^2-4}< =0\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{1}{4}\sqrt{x^2-4}+1< =1\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(x^2-4=0\)
=>\(x^2=4\)
=>\(\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

\(\dfrac{1}{5}\) tấn \(56kg\) \(< 20kg\times34\)
\(\dfrac{3}{4}h< 8400s:3\)
\(\dfrac{1}{5}\) tấn 56 kg = 1000 kg x \(\dfrac{1}{5}\) + 56 kg = 256 kg
20 kg x 34 = 680 kg
Vì 256 kg < 680 kg
Vậy \(\dfrac{1}{5}\) tấn 56 kg < 20 kg x 34
\(\dfrac{3}{4}giờ\) = 3600 giây x \(\dfrac{3}{4}\) = 2700 giây
8400 giây: 3 = 2800 giây
Vì 2700 giây < 2800 giây
Vậy \(\dfrac{3}{4}\) giờ < 8400 giây : 3

Đặt \(BC=x\left(x>5\right)\)
Trong đường tròn (O) có đường kính CD và \(N\in\left(O\right)\) nên \(\widehat{DNC}=90^o\) hay \(\widehat{BND}=90^o\)
Vì BD là tia phân giác của \(\widehat{ABC}\) nên \(\widehat{ABD}=\widehat{NBD}\)
Xét 2 tam giác ABD và NBD vuông tại A và N, có \(\widehat{ABD}=\widehat{NBD}\) và cạnh BD chung nên \(\Delta ABD=\Delta NBD\left(ch-gn\right)\)
\(\Rightarrow BA=BN=5\) \(\Rightarrow NC=BC-BN=5-x\)
Lại có \(\widehat{OMD}=\widehat{ODM}=\widehat{BDA}=\widehat{BDN}\) nên OM//ND (2 góc đồng vị bằng nhau)
Tam giác CND có O là trung điểm DC, OH//DN và \(H\in NC\) nên H là trung điểm NC \(\Rightarrow HC=\dfrac{NC}{2}=\dfrac{x-5}{2}\)
Theo định lý Pythagoras, có \(AC=\sqrt{BC^2-AB^2}=\sqrt{x^2-25}\)
Theo tính chất đường phân giác trong tam giác, ta có:
\(\dfrac{DA}{AB}=\dfrac{DC}{CB}=\dfrac{AC}{AB+CB}\) \(\Rightarrow\dfrac{DA}{5}=\dfrac{DC}{x}=\dfrac{\sqrt{x^2-25}}{x+5}\)
\(\Rightarrow DA=\dfrac{5\sqrt{x^2-5}}{x+5}\) và \(DC=\dfrac{x\sqrt{x^2-5}}{x+5}\)
\(\Rightarrow R_{\left(O\right)}=\dfrac{DC}{2}=\dfrac{x\sqrt{x^2-5}}{2x+10}\)
Lại có \(DN=AD=\dfrac{5\sqrt{x^2-5}}{x+5}\)
\(OH=\dfrac{DN}{2}=\dfrac{5\sqrt{x^2-25}}{2x+10}\) (OH là đường trung bình của tam giác CND)
\(\Rightarrow MH=MO+OH=\dfrac{x\sqrt{x^2-25}}{2x+10}+\dfrac{5\sqrt{x^2-25}}{2x+10}\) \(=\dfrac{\sqrt{x^2-25}}{2}\)
Áp dụng định lý Pythagoras trong tam giác DMC vuông tại M, ta có:
\(MH^2+HC^2=MC^2\)
\(\Leftrightarrow\left(\dfrac{\sqrt{x^2-25}}{2}\right)^2+\left(\dfrac{x-5}{2}\right)^2=18\)
\(\Leftrightarrow\dfrac{x^2-25}{4}+\dfrac{x^2-10x+25}{4}=18\)
\(\Leftrightarrow2x^2-10x=72\)
\(\Leftrightarrow x^2-5x-36=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\left(nhận\right)\\x=-4\left(loại\right)\end{matrix}\right.\)
Vậy \(BC=9\)

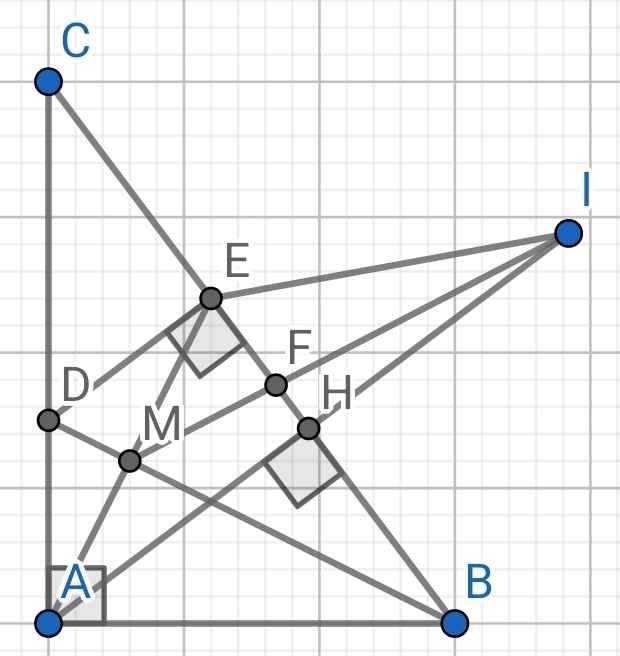
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠EBD
Xét hai tam giác vuông: ∆ABD và ∆EBD có:
BD chung
∠ABD = ∠EBD (cmt)
⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)
b) Do HA = HI (gt)
⇒ H là trung điểm của AI
Mà AH ⊥ BC tại H (gt)
⇒ AI ⊥ BC
⇒ BC là đường trung trực của AI
Mà E ∈ BC
⇒ EA = EI
c) Do ∆ABD = ∆EBD (cmt)
⇒ BA = BE (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AE (1)
Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AE
Mà M là giao điểm của BD và AE
⇒ M là trung điểm của AE
⇒ IM là đường trung tuyến của ∆AIE
Lại có:
H là trung điểm của AE (cmt)
⇒ EH là đường trung tuyến của ∆AIE
∆AIE có:
IM là đường trung tuyến (cmt)
EH là đường trung tuyến (cmt)
Mà IM cắt EH tại F
⇒ F là trọng tâm của ∆AIE
d) Do F là trọng tâm của ∆AIE (cmt)
⇒ HF < HE
⇒ AF < AE (quan hệ giữa đường xiên và hình chiếu)
Lại có:
F nằm trên đường trung trực của AI (do BC là đường trung trực của AI)
⇒ AF = IF
Do F là trọng tâm của ∆AIE (cmt)
⇒ IF = 2MF
Do M là trung điểm của AE (cmt)
⇒ AE = 2ME
Mà AF < AE (cmt)
⇒ AF < 2ME
Mà AF = IF (cmt)
⇒ IF < 2ME
Mà IF = 2MF (cmt)
⇒ 2MF < 2ME
⇒ MF < ME
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔEHA vuông tại H và ΔEHI vuông tại H có
EH chung
HA=HI
Do đó: ΔEHA=ΔEHI
=>EA=EI
c: ΔBAD=ΔBED
=>BA=BE và DA=DE
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại M và M là trung điểm của AE
Xét ΔAEI có
EH,IM là các đường trung tuyến
EH cắt IM tại F
Do đó: F là trọng tâm của ΔAEI

1: \(\left(x-\dfrac{1}{2}\right)+\left(x-\dfrac{1}{4}\right)+\left(x+\dfrac{1}{8}\right)=\dfrac{1}{4}\)
=>\(3x-\dfrac{3}{4}+\dfrac{1}{8}=\dfrac{1}{4}\)
=>\(3x=\dfrac{1}{4}+\dfrac{3}{4}-\dfrac{1}{8}=1-\dfrac{1}{8}=\dfrac{7}{8}\)
=>\(x=\dfrac{7}{24}\)
2: \(112,5\times X-37,25:\dfrac{1}{X}+X\times99,4=34,5\)
=>\(112,5\times X-37,25\times X+99,4\times X=34,5\)
=>\(X\times\left(112,5-37,25+99,4\right)=34,5\)
=>\(X\times174,65=34,5\)
=>\(X=\dfrac{34.5}{174.65}=\dfrac{690}{3493}\)

1: \(\dfrac{1}{26}+\dfrac{-5}{39}=\dfrac{3}{78}-\dfrac{10}{78}=\dfrac{-7}{78}\)
2: \(-\dfrac{1}{16}+\dfrac{-1}{24}=\dfrac{-3}{48}+\dfrac{-2}{48}=-\dfrac{5}{48}\)
3: \(\dfrac{4}{7}-\left(-\dfrac{1}{9}\right)=\dfrac{4}{7}+\dfrac{1}{9}=\dfrac{36}{63}+\dfrac{7}{63}=\dfrac{43}{63}\)
4: \(-0,16+\dfrac{-3}{2}=-0,16-1,5=-1,66\)
5: \(\dfrac{3}{5}-\left(-\dfrac{2}{7}\right)=\dfrac{3}{5}+\dfrac{2}{7}=\dfrac{21}{35}+\dfrac{10}{35}=\dfrac{31}{35}\)
6: \(-\dfrac{4}{12}-\left(-\dfrac{13}{39}-0,25\right)\)
\(=-\dfrac{1}{3}+\dfrac{1}{3}+0,25=0,25\)
7: \(\dfrac{2}{5}-\left(\dfrac{4}{3}+\dfrac{4}{5}\right)-\left(-\dfrac{1}{9}-0,4\right)+\dfrac{11}{9}\)
\(=\dfrac{2}{5}-\dfrac{4}{3}-\dfrac{4}{5}+\dfrac{1}{9}+\dfrac{2}{5}+\dfrac{11}{9}\)
\(=\dfrac{12}{9}-\dfrac{4}{3}=0\)
1. \(\dfrac{1}{26}+\dfrac{-5}{39}=\dfrac{3}{78}+\dfrac{-10}{78}=\dfrac{3-10}{78}=\dfrac{-7}{78}\)
2. \(\dfrac{-1}{16}+\dfrac{-1}{24}=\dfrac{-3}{48}+\dfrac{-2}{48}=\dfrac{-3-2}{48}=\dfrac{-5}{48}\)
3. \(\dfrac{4}{7}-\left(\dfrac{-1}{9}\right)=\dfrac{4}{7}+\dfrac{1}{9}=\dfrac{36}{63}+\dfrac{7}{63}=\dfrac{36+7}{63}=\dfrac{43}{63}\)
4. \(-0.16+\dfrac{-3}{2}=\dfrac{-4}{25}+-\dfrac{3}{2}=\dfrac{-8-75}{50}=\dfrac{-83}{50}\)
5. \(\dfrac{3}{5}-\left(-\dfrac{2}{7}\right)=\dfrac{3}{5}+\dfrac{2}{7}=\dfrac{21}{35}+\dfrac{10}{35}=\dfrac{21+10}{35}=\dfrac{31}{35}\)
6. \(\dfrac{-4}{12}-\left(\dfrac{-13}{39}-0,25\right)+0,75=\dfrac{-1}{3}+\dfrac{1}{3}+0,25+0,75=\left(\dfrac{-1}{3}+\dfrac{1}{3}\right)+\left(0,25+0,75\right)=0+1\)
7. \(2,5-\left(\dfrac{4}{3}+\dfrac{4}{5}\right)-\left(\dfrac{-1}{9}-0,4\right)+\dfrac{11}{9}\)
\(=\dfrac{5}{2}-\dfrac{4}{3}-\dfrac{4}{5}+\dfrac{1}{9}+\dfrac{2}{5}+\dfrac{11}{9}\)
\(=\dfrac{5}{2}-\dfrac{4}{3}-\dfrac{4}{5}+\left(\dfrac{1}{9}+\dfrac{11}{9}\right)+\dfrac{2}{5}\)
\(=\dfrac{5}{2}-\dfrac{4}{3}+\left(\dfrac{2}{5}-\dfrac{4}{5}\right)+\dfrac{12}{9}+\dfrac{2}{5}\)
\(=\dfrac{5}{2}-\dfrac{4}{3}-\dfrac{2}{5}+\dfrac{4}{3}+\dfrac{2}{5}\)
\(=\dfrac{5}{2}\)
I:
Câu 1: \(M=\sqrt{9xy^2}=3\sqrt{xy^2}=3\sqrt{x}\cdot\left|y\right|=-3\sqrt{x}y\)
=>Chọn A
Câu 2: C
Câu 3: B
Câu 4: AC=AD+DC=4+8=12(cm)
Xét ΔBAC vuông tại B có BD là đường cao
nên \(BA^2=AD\cdot AC=4\cdot12=48\)
=>\(BA=4\sqrt{3}\left(cm\right)\)
=>Chọn D
II: Tự luận
Câu 5:
\(\left\{{}\begin{matrix}3x-2y=9\\x-3y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2y=9\\3x-9y=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y-3x+9y=9-30\\x-3y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7y=-21\\x=3y+10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=3\cdot\left(-3\right)+10=10-9=1\end{matrix}\right.\)
Câu 7:
a: \(\text{Δ}=3^2-4\cdot1\cdot\left(m+1\right)\)
=9-4m-4
=-4m+5
Để phương trình có nghiệm thì Δ>=0
=>-4m+5>=0
=>-4m>=-5
=>m<=5/4
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-3\\x_1x_2=\dfrac{c}{a}=m+1\end{matrix}\right.\)
\(A=\left(x_1-x_2\right)^2+5x_1x_2+7m\)
\(=\left(x_1+x_2\right)^2-4x_1x_2+5x_1x_2+7m\)
\(=\left(-3\right)^2+\left(m+1\right)+7m=8m+10\)
=>A không có giá trị lớn nhất