-Nếu các bạn gửi câu trả lời thì kèm theo hình vẽ để dễ hiểu hơn nha (không có cũng không sao)

-Mong các bạn trả lời nhanh cho mình nha vì mai mình phải nộp rồi

2x = 4y   \(\Rightarrow x=2y\)

3y = 2z   \(\Rightarrow z=\dfrac{3}{2}y\)

thay vào phương trình ta được : 

\(2\left(2y\right)^2+3y^2-3\left(\dfrac{3}{2}y\right)^2=12\)

\(\Leftrightarrow8y^2+3y^2-\dfrac{27}{4}y^2=12\)

\(\Leftrightarrow\dfrac{17}{4}y^2=12\)

\(\Leftrightarrow y^2=\dfrac{48}{17}\)

\(\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{4\sqrt{51}}{17}\\y=\dfrac{-4\sqrt{51}}{17}\end{matrix}\right.\)

\(y=\dfrac{4\sqrt{51}}{17}\Rightarrow x=\dfrac{8\sqrt{51}}{17};z=\dfrac{6\sqrt{51}}{17}\)

\(y=-\dfrac{4\sqrt{51}}{17}\Rightarrow x=-\dfrac{8\sqrt{51}}{17};z=-\dfrac{6\sqrt{51}}{17}\)

sai

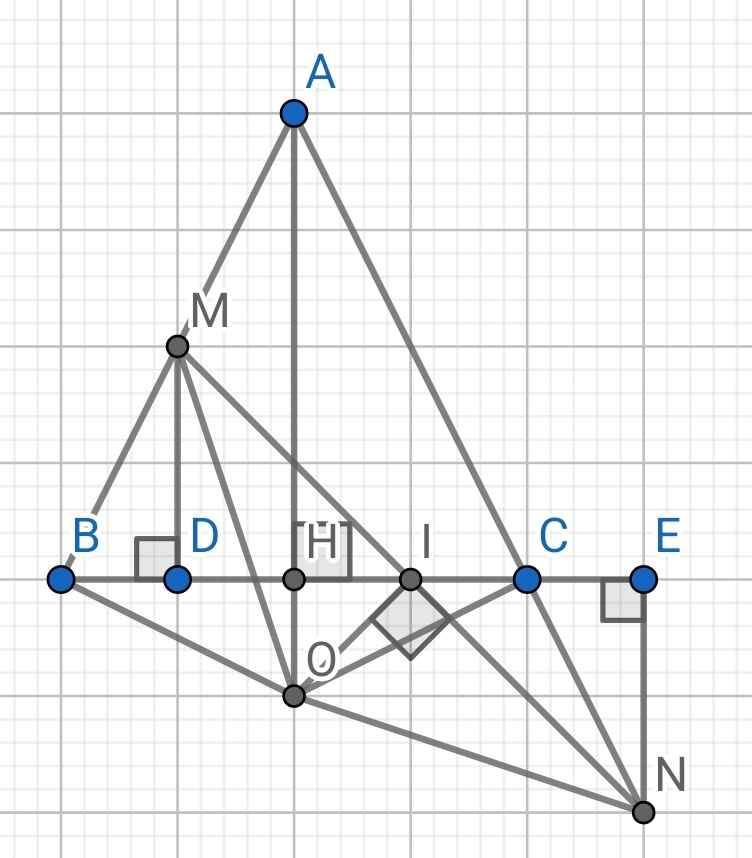 a) ∆ABC cân tại A

⇒ ∠ABC = ∠ACB

Mà ∠ACB = ∠ECN (đối đỉnh)

⇒ ∠ABC = ∠ECN

⇒ ∠DBM = ∠ECN

Xét hai tam giác vuông: ∆DBM và ∆ECN có:

BD = CE (gt)

∠DBM = ∠ECN (cmt)

⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)

⇒ DM = EN (hai cạnh tương ứng)

b) Do DM ⊥ BC (gt)

EN ⊥ BC (gt)

⇒ DM // EN

⇒ ∠DMI = ∠ENI (so le trong)

Xét hai tam giác vuông: ∆DMI và ∆ENI có:

DM = EN (cmt)

∠DMI = ∠ENI (cmt)

⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)

⇒ MI = NI (hai cạnh tương ứng)

⇒ I là trung điểm của MN

⇒ BC cắt MN tại trung điểm I của MN

c) Do AH ⊥ BC nên AH là đường cao của ∆ABC

Mà ∆ABC cân tại A

AH cũng là đường phân giác của ∆ABC

⇒ ∠BAH = ∠CAH

⇒ ∠BAO = ∠CAO

Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét ∆OAB và ∆OAC có:

OA là cạnh chung

∠BAO = ∠CAO (cmt)

AB = AC (cmt)

⇒ ∆OAB = ∆OAC (c-g-c)

⇒ OB = OC (hai cạnh tương ứng)

Ta có:

I là trung điểm MN (cmt)

OI ⊥ MN (gt)

⇒ OI là đường trung trực của MN

⇒ OM = ON

Do ∆DBM = ∆ECN (cmt)

⇒ BM = CN (hai cạnh tương ứng)

Xét ∆OBM và ∆OCN có:

OB = OC (cmt)

OM = ON (cmt)

BM = CN (cmt)

⇒ ∆OBM = ∆OCN (c-c-c)

d) Do ∆OBM = ∆OCN (cmt)

⇒ ∠OBM = ∠OCN (hai góc tương ứng)

Do ∆OAB = ∆OAC (cmt)

⇒ ∠OBA = ∠OCA (hai góc tương ứng)

⇒ ∠OBM = ∠OCA

Mà ∠OBM = ∠OCN (cmt)

⇒ ∠OCN = ∠OCA

Mà ∠OCN + ∠OCA = 180⁰ (kề bù)

⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰

⇒ OC ⊥ AC

 a) ∆ABC cân tại A

⇒ ∠ABC = ∠ACB

Mà ∠ACB = ∠ECN (đối đỉnh)

⇒ ∠ABC = ∠ECN

⇒ ∠DBM = ∠ECN

Xét hai tam giác vuông: ∆DBM và ∆ECN có:

BD = CE (gt)

∠DBM = ∠ECN (cmt)

⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)

⇒ DM = EN (hai cạnh tương ứng)

b) Do DM ⊥ BC (gt)

EN ⊥ BC (gt)

⇒ DM // EN

⇒ ∠DMI = ∠ENI (so le trong)

Xét hai tam giác vuông: ∆DMI và ∆ENI có:

DM = EN (cmt)

∠DMI = ∠ENI (cmt)

⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)

⇒ MI = NI (hai cạnh tương ứng)

⇒ I là trung điểm của MN

⇒ BC cắt MN tại trung điểm I của MN

c) Do AH ⊥ BC nên AH là đường cao của ∆ABC

Mà ∆ABC cân tại A

AH cũng là đường phân giác của ∆ABC

⇒ ∠BAH = ∠CAH

⇒ ∠BAO = ∠CAO

Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét ∆OAB và ∆OAC có:

OA là cạnh chung

∠BAO = ∠CAO (cmt)

AB = AC (cmt)

⇒ ∆OAB = ∆OAC (c-g-c)

⇒ OB = OC (hai cạnh tương ứng)

Ta có:

I là trung điểm MN (cmt)

OI ⊥ MN (gt)

⇒ OI là đường trung trực của MN

⇒ OM = ON

Do ∆DBM = ∆ECN (cmt)

⇒ BM = CN (hai cạnh tương ứng)

Xét ∆OBM và ∆OCN có:

OB = OC (cmt)

OM = ON (cmt)

BM = CN (cmt)

⇒ ∆OBM = ∆OCN (c-c-c)

d) Do ∆OBM = ∆OCN (cmt)

⇒ ∠OBM = ∠OCN (hai góc tương ứng)

Do ∆OAB = ∆OAC (cmt)

⇒ ∠OBA = ∠OCA (hai góc tương ứng)

⇒ ∠OBM = ∠OCA

Mà ∠OBM = ∠OCN (cmt)

⇒ ∠OCN = ∠OCA

Mà ∠OCN + ∠OCA = 180⁰ (kề bù)

⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰

⇒ OC ⊥ AC

a) ∆ABC cân tại A

⇒ ∠ABC = ∠ACB

Mà ∠ACB = ∠ECN (đối đỉnh)

⇒ ∠ABC = ∠ECN

⇒ ∠DBM = ∠ECN

Xét hai tam giác vuông: ∆DBM và ∆ECN có:

BD = CE (gt)

∠DBM = ∠ECN (cmt)

⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)

⇒ DM = EN (hai cạnh tương ứng)

b) Do DM ⊥ BC (gt)

EN ⊥ BC (gt)

⇒ DM // EN

⇒ ∠DMI = ∠ENI (so le trong)

Xét hai tam giác vuông: ∆DMI và ∆ENI có:

DM = EN (cmt)

∠DMI = ∠ENI (cmt)

⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)

⇒ MI = NI (hai cạnh tương ứng)

⇒ I là trung điểm của MN

⇒ BC cắt MN tại trung điểm I của MN

c) Do AH ⊥ BC nên AH là đường cao của ∆ABC

Mà ∆ABC cân tại A

AH cũng là đường phân giác của ∆ABC

⇒ ∠BAH = ∠CAH

⇒ ∠BAO = ∠CAO

Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét ∆OAB và ∆OAC có:

OA là cạnh chung

∠BAO = ∠CAO (cmt)

AB = AC (cmt)

⇒ ∆OAB = ∆OAC (c-g-c)

⇒ OB = OC (hai cạnh tương ứng)

Ta có:

I là trung điểm MN (cmt)

OI ⊥ MN (gt)

⇒ OI là đường trung trực của MN

⇒ OM = ON

Do ∆DBM = ∆ECN (cmt)

⇒ BM = CN (hai cạnh tương ứng)

Xét ∆OBM và ∆OCN có:

OB = OC (cmt)

OM = ON (cmt)

BM = CN (cmt)

⇒ ∆OBM = ∆OCN (c-c-c)

d) Do ∆OBM = ∆OCN (cmt)

⇒ ∠OBM = ∠OCN (hai góc tương ứng)

Do ∆OAB = ∆OAC (cmt)

⇒ ∠OBA = ∠OCA (hai góc tương ứng)

⇒ ∠OBM = ∠OCA

Mà ∠OBM = ∠OCN (cmt)

⇒ ∠OCN = ∠OCA

Mà ∠OCN + ∠OCA = 180⁰ (kề bù)

⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰

⇒ OC ⊥ AC

\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)

Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:

\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)

\(\dfrac{9y^2}{25}-y^2=-4\)

\(-\dfrac{16}{25}y^2=-4\)

\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)

\(y^2=\dfrac{25}{4}\)

\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)

*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)

*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)

Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:

\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)

ai biết gì đâu