 Giúp tớ bài 6, 10 nhé. Mình đang gấp
Giúp tớ bài 6, 10 nhé. Mình đang gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
b: E đối xứng M qua AC
=>AC là đường trung trực của EM
=>AE=AM; CE=CM
ΔBAC vuông tại A
mà AM là đường trung tuyến
nên AM=CM=MB
AM=CM
AE=AM
CE=CM
Do đó: AM=MC=CE=AE
=>AMCE là hình thoi
c: AMCE là hình thoi
=>AE//CM
=>AE//BM
Xét tứ giác ABME có
AE//BM
AE=BM
Do đó: ABME là hình bình hành
=>AM cắt BE tại trung điểm của mỗi đường
mà I là trung điểm của AM
nên I là trung điểm của BE
=>B,I,E thẳng hàng

a: \(\left\{{}\begin{matrix}1,7x-2y=3,8\\2,1x+5y=0,4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8,5x-10y=19\\4,2x+10y=0,8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12,7x=19,8\\1,7x-2y=3,8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{198}{127}\\2y=1,7x-3,8=-\dfrac{146}{127}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{198}{127}\\y=-\dfrac{73}{127}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\left(\sqrt{5}+2\right)x+y=3-\sqrt{5}\\-x+2y=6-2\sqrt{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(2\sqrt{5}+4\right)x+2y=6-2\sqrt{5}\\-x+2y=6-2\sqrt{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(2\sqrt{5}+4+1\right)=0\\2y=x+6-2\sqrt{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\2y=6-2\sqrt{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=3-\sqrt{5}\end{matrix}\right.\)

Gọi vận tốc trung bình ở lượt đi của nhóm bạn là: x (km/giờ) (ĐK:x>4)
=> vận tốc trung bình ở lượt về của nhóm bạn là: x-4 (km/giờ)
Thời gian lúc đi từ A đến B là: 24/x (giờ)
Thời gian lúc về từ B về A là: 24/x-4 (giờ)
Theo đề: Thời gian về lâu hơn thời gian đi 1 giờ nên ta có pt:
\(\dfrac{24}{x-4}-\dfrac{24}{x}=1\\ \Leftrightarrow\dfrac{24x-24\left(x-4\right)}{x\left(x-4\right)}=1\\ \Leftrightarrow24x-24x+96=x\left(x-4\right)\\ \Leftrightarrow x^2-4x=96\\ \Leftrightarrow x^2-4x-96=0\\ \Leftrightarrow\left(x-12\right)\left(x+8\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-12=0\\x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=12\left(nhận\right)\\x=-8\left(loại\right)\end{matrix}\right.\)
Vậy vận tốc tb ở lượt đi là: 12km/h
Đáp án: 12km/h
Giải thích các bước giải:
gọi x là tốc độ trung bình bàn đầu (km/h)
-> tốc độ trung bình lúc sau: x-4 (km/h)
vì thời gian xe đi từ B về A chậm hơn 1 giờ nên ta có phương trình:
24/x-4 - 24/x = 1
( bạn tự tính giúp mình, mình bấm máy thôi)
-> x= 12
-> tốc độ tb ban đầu là 12 km/h


1: Xét ΔEBA vuông tại B và ΔEDF vuông tại D có
\(\widehat{BEA}\) chung
Do đó: ΔEBA~ΔEDF
2: Xét ΔIDA vuông tại D và ΔIBF vuông tại B có
\(\widehat{DIA}=\widehat{BIF}\)(hai góc đối đỉnh)
Do đó: ΔIDA~ΔIBF
=>\(\dfrac{ID}{IB}=\dfrac{IA}{IF}\)
=>\(ID\cdot IF=IA\cdot IB\)

1: 7-(x-3)=2(3-4x)
=>7-x+3=6-8x
=>-x+10=6-8x
=>-x+8x=6-10
=>7x=-4
=>\(x=-\dfrac{4}{7}\)
2: ĐKXĐ: \(x\notin\left\{1;3\right\}\)
\(\dfrac{3x}{x-1}=\dfrac{2x}{x-3}-\dfrac{4x}{\left(x-1\right)\left(x-3\right)}\)
=>\(\dfrac{3x\left(x-3\right)}{\left(x-1\right)\left(x-3\right)}=\dfrac{2x\left(x-1\right)}{\left(x-3\right)\left(x-1\right)}-\dfrac{4x}{\left(x-1\right)\left(x-3\right)}\)
=>\(3x^2-9x=2x^2-2x-4x\)
=>\(3x^2-9x=2x^2-6x\)
=>\(x^2-3x=0\)
=>x(x-3)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=3\left(loại\right)\end{matrix}\right.\)
3: \(2\left(3x+1\right)-3\left(5x+2\right)>2x-9\)
=>6x+2-15x-6>2x-9
=>-9x-4>2x-9
=>-11x>-5
=>\(x< \dfrac{5}{11}\)

1: |2x-1|=3
=>\(\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2x=4\\2x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)
Thay x=-1 vào A, ta được:
\(A=\dfrac{-1-1}{\left(-1\right)^2-4}=\dfrac{-2}{1-4}=\dfrac{-2}{-3}=\dfrac{2}{3}\)
2: \(B=\dfrac{x-3}{x-2}-\dfrac{3}{x+2}-\dfrac{4x+5}{4-x^2}\)
\(=\dfrac{x-3}{x-2}-\dfrac{3}{x+2}+\dfrac{4x+5}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{\left(x-3\right)\left(x+2\right)-3\left(x-2\right)+4x+5}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2-x-6-3x+6+4x+5}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+5}{x^2-4}\)
3: \(\dfrac{A}{B}< 0\)
=>\(\dfrac{x-1}{x^2-4}:\dfrac{x^2+5}{x^2-4}< 0\)
=>\(\dfrac{x-1}{x^2+5}< 0\)
=>x-1<0
=>x<1
Kết hợp ĐKXĐ, ta được:
\(\left\{{}\begin{matrix}x< 1\\x\ne-2\end{matrix}\right.\)
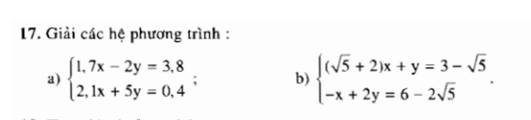


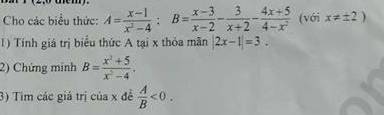
8)
a) \(A=1-\dfrac{x}{1-\dfrac{x}{x+1}}\left(x\ne-1\right)\)
\(=1-\dfrac{x}{\dfrac{x+1-x}{x+1}}=1-\dfrac{x}{\dfrac{1}{x+1}}=1-x\left(x+1\right)=-x^2-x+1\)
b) \(B=\dfrac{\dfrac{x}{y}+\dfrac{y}{x}}{\dfrac{x-y}{x+y}+\dfrac{x+y}{x-y}}=\dfrac{\dfrac{x^2}{xy}+\dfrac{y^2}{xy}}{\dfrac{\left(x-y\right)^2+\left(x+y\right)^2}{\left(x+y\right)\left(x-y\right)}}\left(x\ne\pm y;x\ne0;y\ne0\right)\)
\(=\dfrac{\dfrac{x^2+y^2}{xy}}{\dfrac{x^2-2xy+y^2+x^2+2xy+y^2}{\left(x+y\right)\left(x-y\right)}}=\dfrac{\dfrac{x^2+y^2}{xy}}{\dfrac{2\left(x^2+y^2\right)}{x^2-y^2}}\)
\(=\dfrac{x^2+y^2}{xy}\cdot\dfrac{x^2-y^2}{2\left(x^2+y^2\right)}=\dfrac{x^2-y^2}{2xy}\)
10:
a: Thời gian dự định là \(\dfrac{60}{x}\left(giờ\right)\)
b: Thời gian đi nửa quãng đường đầu tiên là: \(\dfrac{60}{2}:\left(x+10\right)=\dfrac{30}{x+10}\left(giờ\right)\)
Thời gian đi nửa quãng đường còn lại là:
\(\dfrac{60-30}{x-6}=\dfrac{30}{x-6}\left(giờ\right)\)
c: Ô tô đến B đúng giờ nên ta có: \(\dfrac{30}{x+10}+\dfrac{30}{x-6}=\dfrac{60}{x}\)
=>\(\dfrac{1}{x+10}+\dfrac{1}{x-6}=\dfrac{2}{x}\)
=>\(\dfrac{x-6+x+10}{\left(x+10\right)\left(x-6\right)}=\dfrac{2}{x}\)
=>\(\dfrac{2x+4}{\left(x+10\right)\left(x-6\right)}=\dfrac{2}{x}\)
=>\(\dfrac{x+2}{x^2+4x-60}=\dfrac{1}{x}\)
=>\(x\left(x+2\right)=x^2+4x-60\)
=>\(x^2+2x=x^2+4x-60\)
=>-2x=-60
=>x=30
Vậy: Vận tốc dự định của ô tô là 30km/h
Bài 6:
a: \(A=\dfrac{x-1}{x}-\dfrac{x+1}{x^2-x}+\dfrac{3\left(x-1\right)}{x^2-2x+1}\)
\(=\dfrac{x-1}{x}-\dfrac{x+1}{x\left(x-1\right)}+\dfrac{3}{x-1}\)
\(=\dfrac{\left(x-1\right)\left(x-1\right)-x-1+3x}{\left(x-1\right)\cdot x}\)
\(=\dfrac{x^2-2x+1+2x-1}{x\left(x-1\right)}=\dfrac{x^2}{x\left(x-1\right)}=\dfrac{x}{x-1}\)
b: \(B=\dfrac{x+y}{2\left(x-y\right)}-\dfrac{x-y}{2\left(x+y\right)}+\dfrac{2y^2}{x^2-y^2}\)
\(=\dfrac{\left(x+y\right)^2-\left(x-y\right)^2+4y^2}{2\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x^2+2xy+y^2-x^2+2xy-y^2+4y^2}{2\left(x-y\right)\left(x+y\right)}=\dfrac{4y^2+4xy}{2\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{2y\left(x+y\right)}{2\left(x-y\right)\left(x+y\right)}=\dfrac{y}{x-y}\)