Chữ cái có tâm đối xứng là O,H

Chữ cái có trục đối xứng là T,H,O

SOS;-;

                       Giải:

Gọi số học sinh tham gia lao động hôm qua là y (học sinh); y \(\in\) N*

Số học sinh khối 6 tham gia lao động hôm qua là: 40%y

Số học sinh khối 6 tham gia lao động hôm nay là: 

              (100% - 75%). 40%\(x\) = 10%y

Số học sinh tham gia lao động hôm qua của  khối 7 là: 36%y

Số học sinh tham gia lao động hôm nay của khối 7 là: 

              (100% + 48%).36%y = 53,28%y

Số học sinh tham gia lao động hôm qua của khối 8 là: 

              100% y - 40%y - 36%y = 24%y

Số học sinh tham gia lao động hôm nay của khối 8 là:

               (100% + 75%). 24%y = 42%y

Tổng số học sinh tham gia lao động hôm nay là:

              10%y + 53,28%y + 42%y = 105,28%y

  Vậy tổng số học sinh tham gia lao động hôm nay đã tăng so với hôm qua là:

               105,28% - 100% = 5,28%

Kết luận: Vậy tổng số học sinh tham gia lao động hôm nay tăng so với hôm qua là 5,28%

+ �=131+132+133+…+160S=311​+321​+331​+…+601​

�<(130+130+…+130)+(140+140+…+140)+(150+150+…+150)S<(301​+301​+…+301​)+(401​+401​+…+401​)+(501​+501​+…+501​)

�<1030+1040+1050<4860=45;S<3010​+4010​+5010​<6048​=54​;

+ �>(140+140+…+140)+(150+150+…+150)+(160+160+…+160)S>(401​+401​+…+401​)+(501​+501​+…+501​)+(601​+601​+…+601​)

�>1040+1050+1060>35.S>4010​+5010​+6010​>53​.

a: Số quả bóng bán được trong tháng 1 là \(3\cdot5=15\left(quả\right)\)

Số quả bóng bán được trong tháng 2 là \(4\cdot5=20\left(quả\right)\)

Số quả bóng bán được trong tháng 3 là \(2\cdot5=10\left(quả\right)\)

b: Tổng số quả bóng rổ bán được trong 3 tháng là:

15+20+10=45(quả)

c: Tháng 2 bán được nhiều hơn tháng 3:

20-10=10(quả)

d: Tỉ số giữa số lượng bóng rổ bán được trong tháng 1 và tháng 2 là:

\(15:20=\dfrac{3}{4}\)

a) Số lượng bóng rổ bán được trong tháng 1, tháng 2, tháng 3 lần lượt là:

$15$ quả; $20$ quả; $10$ quả.

b) Cả ba tháng cửa hàng bán được:

$15+20+10=45$ (quả)

c) Tháng 2 cửa hàng bán được nhiều hơn tháng 3:

$20–10=10$ (quả)

d) Tỉ số giữa số lượng bóng bán được trong tháng 1 và tháng 2 là:

3:4=343:4=43​
 

bài 1:

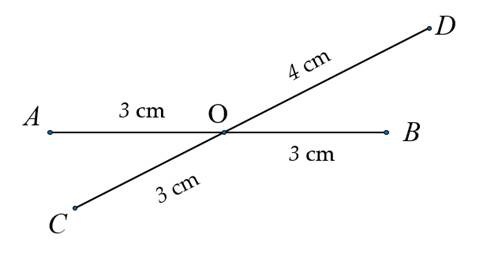
a: O thuộc đoạn AB,CD,OA,OB,OC,OD

b: O là trung điểm của AB

1. a) $O$ thuộc các đoạn thẳng: $AB;CD;OA;OB;OC;OD.$

b) Ta có $O$ nằm giữa hai điểm $A$ và $B$ và $OA=OB=3$ cm nên $O$ là trung điểm của đoạn thẳng $AB.$

2. a) Số đo góc $xOy$ bằng 30∘30∘.

b)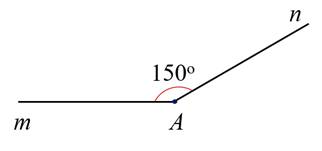 

a) \(\dfrac{5}{17}-\dfrac{25}{31}+\dfrac{12}{17}+\dfrac{-6}{31}\)

\(=\left(\dfrac{5}{17}+\dfrac{12}{17}\right)+\left(\dfrac{-25}{31}+\dfrac{-6}{31}\right)\)

\(=\dfrac{17}{17}+\dfrac{-31}{31}\)

\(=1+\left(-1\right)=0\)

b) \(\dfrac{17}{8}:\left(\dfrac{27}{8}+\dfrac{11}{4}\right)\)

\(=\dfrac{17}{8}:\left(\dfrac{27}{8}+\dfrac{22}{8}\right)\)

\(=\dfrac{17}{8}:\dfrac{49}{8}=\dfrac{17}{8}\cdot\dfrac{8}{49}=\dfrac{17}{49}\)

c) \(\dfrac{1}{5}\cdot\dfrac{11}{16}+\dfrac{1}{5}\cdot\dfrac{5}{16}+\dfrac{4}{5}\)

\(=\dfrac{1}{5}\cdot\left(\dfrac{11}{16}+\dfrac{5}{16}+4\right)\)

\(=\dfrac{1}{5}\cdot\left(\dfrac{16}{16}+4\right)\)

\(=\dfrac{1}{5}\cdot\left(1+4\right)=\dfrac{1}{5}\cdot5=1\)

d) \(\dfrac{5}{6}:25-2+\dfrac{-7}{3}\cdot\dfrac{2}{7}\)

\(=\dfrac{5}{6}\cdot\dfrac{1}{25}-2+\dfrac{-2}{3}\)

\(=\dfrac{1}{30}-\dfrac{6}{3}+\dfrac{-2}{3}\)

\(=\dfrac{1}{30}-\dfrac{8}{3}=\dfrac{1}{30}-\dfrac{80}{30}=\dfrac{-79}{30}\)

a) 517−2531+1217+−631175​−3125​+1712​+31−6​

=517−2531+1217+−631=175​−3125​+1712​+31−6​

=(517+1217)+(−2531+−631)=(175​+1712​)+(−3125​+31−6​)

$=1+(-1)$

$=0$

b) 178:(278+114)817​:(827​+411​)

=178:(278+228)=817​:(827​+822​)

=178:498=817​:849​

=1749=4917​.

c) 15⋅1116+15⋅516+4551​⋅1611​+51​⋅165​+54​

=15⋅(1116+516)+45=51​⋅(1611​+165​)+54​

=15⋅1+45=51​⋅1+54​

=15+45=1.=51​+54​=1.

d) 56:25−2+−73⋅2765​:25−2+3−7​⋅72​

=56:25−2+−73⋅27=65​:25−2+3−7​⋅72​

=56⋅125−2+−23=65​⋅251​−2+3−2​

=130−2+−23=301​−2+3−2​

=130−6030+−2030=301​−3060​+30−20​

=130−6030+−2030=−7930=301​−3060​+30−20​=30−79​
 

               Bài 2:

Trên hình vẽ có 10 góc chung đỉnh 0. Đó là những góc

 \(\widehat{xom}\); \(\widehat{xon}\); \(\widehat{xop}\); \(\widehat{xoy}\); \(\widehat{mon}\); \(\widehat{mop}\); \(\widehat{moy}\); \(\widehat{nop}\); \(\widehat{noy}\); \(\widehat{poy}\)

Điểm P là điểm trong của góc mon; mop; xoy

Điểm Q là điểm trong của góc yop; yon; yom; yox

a: Giá của một lít xăng trước khi tăng là:

\(23000\cdot\dfrac{100}{110}=\dfrac{230000}{11}\left(đồng\right)\)

b: Sau 1 năm thì số tiền lãi ông Nam nhận được là:

\(500000000\cdot7,5\%=37500000\left(đồng\right)\)

Tổng số tiền nhận được là:

500000000+37500000=537500000(đồng)

Gọi số cần tìm là abcde 

Số khi viết thêm chữ số 2 vào đằng sau là abcde2

Số viết thêm chữ số 2 vào đằng trước là 2abcde

Ta có :

2abcde x 3 = abcde2

( 200000 + abcde ) x 3 = abcde x 10 + 2

200000 x 3 + abcde x 3 = abcde x 10 + 2

600000 + abcde x 3 = abcde x 10 + 2

600000 - 2                = abcde x 10 - abcde x 3

599998                     = abcde x 7

abcde                       = 59998 : 7

abcde                       = 85714

→ Số cần tìm là 85714

chỗ 59998 : 7 mik vt nhầm 599998 : 7 nha