Gọi số cần tìm có dạng là \(X=\overline{ab}\)

Khi viết thêm chữ số 0 vào giữa hai chữ số thì ta được số mới gấp 6 lần số cũ nên \(\overline{a0b}=6\cdot\overline{ab}\)

=>\(100a+b=6\left(10a+b\right)\)

=>100a+b=60a+6b

=>40a=5b

=>8a=b

=>b=8; a=1

Vậy: Số cần tìm là 18

Bài 8:

1: \(\left(x+y\right)^2-\left(x-y\right)^2\)

\(=\left(x+y+x-y\right)\left(x+y-x+y\right)\)

\(=2x\cdot2y=4xy\)

2: \(\left(2x+3\right)^2-3x\left(2x+1\right)\)

\(=4x^2+12x+9-6x^2-3x\)

\(=-2x^2+9x+9\)

3: \(\left(4-2x\right)\left(4+2x\right)-4x\left(2x+3\right)\)

\(=4^2-\left(2x\right)^2-8x^2-12x\)

\(=16-4x^2-8x^2-12x=-12x^2-12x+16\)

4: \(2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2-2x^2\)

\(=2\left(x^2-y^2\right)+x^2+2xy+y^2-2x^2\)

\(=2x^2-2y^2-x^2+2xy+y^2=x^2+2xy-y^2\)

5: \(\left(3x+4\right)\left(3x-2\right)-\left(3x+1\right)^2\)

\(=9x^2-6x+12x-8-9x^2-6x-1\)

=-9

6: \(4x\left(x-3\right)-\left(2x-1\right)\left(2x+1\right)\)

\(=4x^2-12x-\left(4x^2-1\right)\)

\(=4x^2-12x-4x^2+1=-12x+1\)

7: \(\dfrac{3}{2}x^2-\left(x-1\right)\left(x+1\right)+3x\)

\(=\dfrac{3}{2}x^2+3x-\left(x^2-1\right)\)

\(=\dfrac{3}{2}x^2+3x-x^2+1=\dfrac{1}{2}x^2+3x+1\)

8: \(2\left(5-x\right)\left(5+x\right)-\left(2x+3\right)^2-x\left(3x+2\right)\)

\(=2\left(25-x^2\right)-4x^2-12x-9-3x^2-2x\)

\(=2\left(25-x^2\right)-7x^2-14x-9\)

\(=50-2x^2-7x^2-14x-9=-9x^2-14x+41\)

Giúp tớ nhanh vs ạ

Bài 8:

\(1)\left(x+y\right)^2-\left(x-y\right)^2\\ =\left(x^2+2xy+y^2\right)-\left(x^2-2xy+y^2\right)\\ =x^2+2xy+y^2-x^2+2xy-y^2\\ =4xy\\ 2)\left(2x+3\right)^2-3x\left(2x+1\right)\\ =\left(4x^2+12x+9\right)-\left(6x^2+3x\right)\\ =4x^2+12x+9-6x^2-3x\\ =-2x^2+9x+9\\ 3)\left(4-2x\right)\left(4+2x\right)-4x\left(2x+3\right)\\ =\left[4^2-\left(2x\right)^2\right]-\left(8x^2+12x\right)\\ =16-4x^2-8x^2-12x\\ =16-12x^2-12x\\ 4)2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2-2x^2\\ =2\left(x^2-y^2\right)+\left(x^2+2xy+y^2\right)-2x^2\\ =2x^2-2y^2+x^2+2xy+y^2-2x^2\\ =x^2+2xy-y^2\)

Bài 8:

1: \(\left(x+y\right)^2-\left(x-y\right)^2\)

\(=\left(x+y+x-y\right)\left(x+y-x+y\right)\)

\(=2x\cdot2y=4xy\)

2: \(\left(2x+3\right)^2-3x\left(2x+1\right)\)

\(=4x^2+12x+9-6x^2-3x\)

\(=-2x^2+9x+9\)

3: \(\left(4-2x\right)\left(4+2x\right)-4x\left(2x+3\right)\)

\(=4^2-\left(2x\right)^2-8x^2-12x\)

\(=16-4x^2-8x^2-12x=-12x^2-12x+16\)

4: \(2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2-2x^2\)

\(=2\left(x^2-y^2\right)+x^2+2xy+y^2-2x^2\)

\(=2x^2-2y^2-x^2+2xy+y^2=x^2+2xy-y^2\)

5: \(\left(3x+4\right)\left(3x-2\right)-\left(3x+1\right)^2\)

\(=9x^2-6x+12x-8-9x^2-6x-1\)

=-9

6: \(4x\left(x-3\right)-\left(2x-1\right)\left(2x+1\right)\)

\(=4x^2-12x-\left(4x^2-1\right)\)

\(=4x^2-12x-4x^2+1=-12x+1\)

7: \(\dfrac{3}{2}x^2-\left(x-1\right)\left(x+1\right)+3x\)

\(=\dfrac{3}{2}x^2+3x-\left(x^2-1\right)\)

\(=\dfrac{3}{2}x^2+3x-x^2+1=\dfrac{1}{2}x^2+3x+1\)

8: \(2\left(5-x\right)\left(5+x\right)-\left(2x+3\right)^2-x\left(3x+2\right)\)

\(=2\left(25-x^2\right)-4x^2-12x-9-3x^2-2x\)

\(=2\left(25-x^2\right)-7x^2-14x-9\)

\(=50-2x^2-7x^2-14x-9=-9x^2-14x+41\)

11.

a) 

\(A=\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)\\=\left(x+1\right)\left(x^2-x\cdot1+1^2\right)-\left(x-1\right)\left(x^2+x\cdot1+1^2\right)\\ =\left(x^3+1^3\right)-\left(x^3-1^3\right)\\ =x^3+1-x^3+1\\ =2\)

=> Giá trị của bt không phụ thuộc vào biến 

b) 

\(B=\left(2x+6\right)\left(4x^2-12x+36\right)-8x^3+10\\ =\left(2x+6\right)\left[\left(2x\right)^2-2x\cdot6+6^2\right]-8x^3+10\\ =\left[\left(2x\right)^3+6^3\right]-8x^3+10\\ =\left(8x^3+216\right)-8x^3+10\\ =8x^3+216-8x^3+10\\ =226\)

=> Giá trị của bt không phụ thuộc vào biến

6.

\(a)\left(x+1\right)^3=x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3=x^3+3x^2+3x+1\\ b)\left(2x+3\right)^3=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot3+3\cdot2x\cdot3^2+3^3=8x^3+36x^2+54x+27\\ c)\left(x^2+2\right)^3=\left(x^2\right)^3+3\cdot\left(x^2\right)^2\cdot2+3\cdot x^2\cdot2^2+2^3=x^6+6x^4+12x^2+8\\ d)\left(2x+5y\right)^3=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot5y+3\cdot2x\cdot\left(5y\right)^2+\left(5y\right)^3=8x^3+60x^2y+150xy^2+125y^3\\ e.\left(x+\dfrac{1}{2}\right)^3=x^3+3\cdot x^2\cdot\dfrac{1}{2}+3\cdot x\cdot\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3=x^3+\dfrac{3}{2}x^2+\dfrac{3}{4}x+\dfrac{1}{8}\\ g.\left(\dfrac{1}{2}x+y^2\right)=\left(\dfrac{1}{2}x\right)^3+3\cdot\left(\dfrac{1}{2}x\right)^2\cdot y^2+3\cdot\dfrac{1}{2}x\cdot\left(y^2\right)^2+\left(y^2\right)^3\\ =\dfrac{x^3}{8}+\dfrac{3}{4}x^2y^2+\dfrac{3}{2}xy^4+y^6\\ h.\left(x^2-2\right)^3=\left(x^2\right)^3-3\cdot\left(x^2\right)^2\cdot2+3\cdot x^2\cdot2^2-2^3=x^6-6x^4+12x^2-8\)

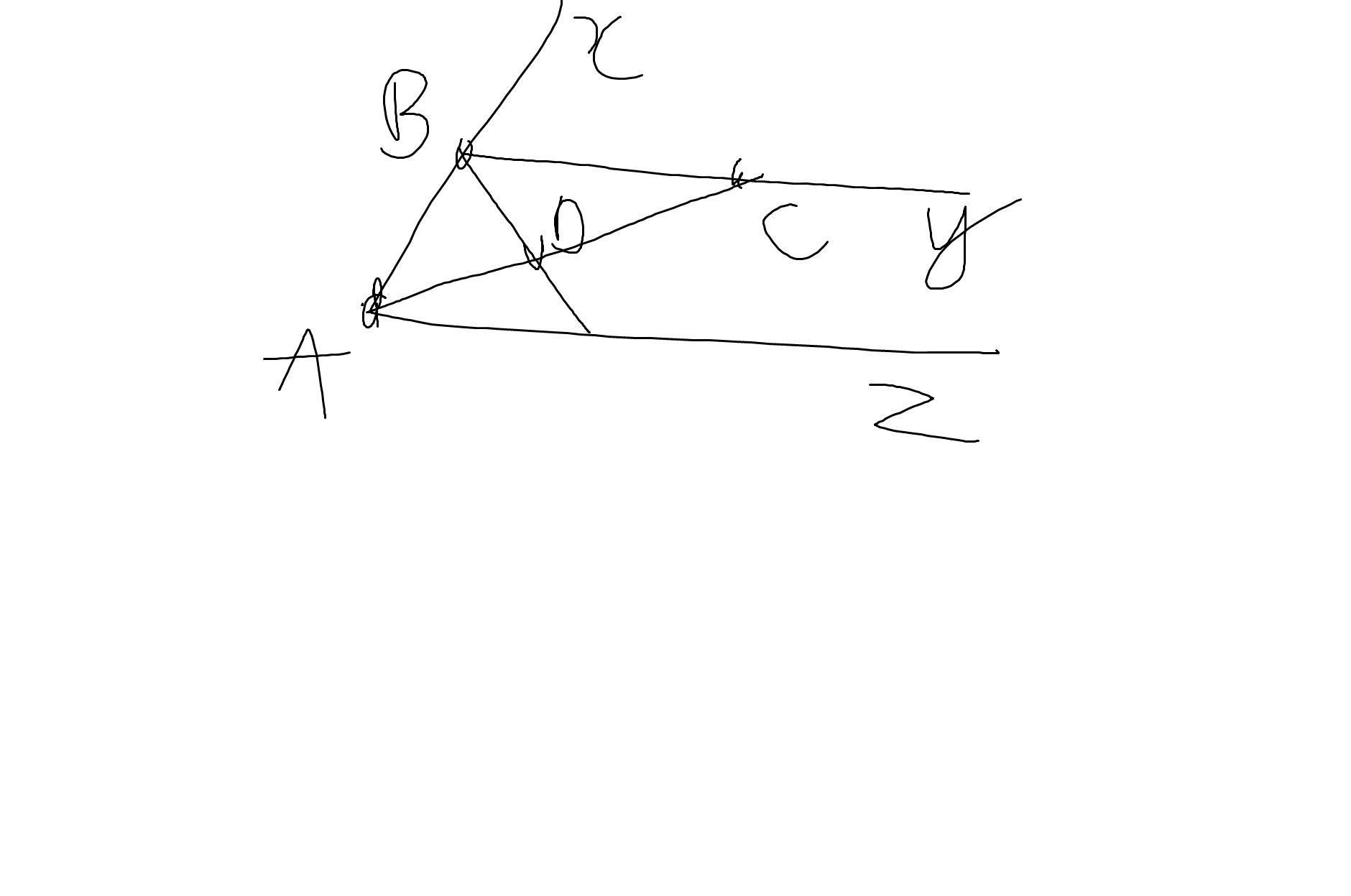
a: Ta có: \(\widehat{xBy}=\widehat{xAz}\left(=60^0\right)\)

mà hai góc này là hai góc ở vị trí đồng vị

nên By//Az

b: Ta có: \(\widehat{ABC}+\widehat{xBC}=180^0\)(hai góc kề bù)

=>\(\widehat{ABC}+60^0=180^0\)

=>\(\widehat{ABC}=120^0\)

AC là phân giác của góc zAB

=>\(\widehat{BAC}=\dfrac{\widehat{xAB}}{2}=30^0\)

Xét ΔBAC có \(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^0\)

=>\(\widehat{BCA}+120^0+30^0=180^0\)

=>\(\widehat{BCA}=30^0\)

c: Ta có: BD là phân giác của góc ABC

=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=60^0\)

Xét ΔDBA có \(\widehat{DBA}+\widehat{DAB}=60^0+30^0=90^0\)

nên ΔBDA vuông tại D

=>BD\(\perp\)AC

Kẻ Ex // AB 

 \(\widehat{BEx}\) = \(\widehat{CBA}\) = 49⁰  (đồng vị)

\(\widehat{xEF}\) + \(\widehat{EFG}\)  = 180⁰ (hai góc trong cùng phía)

⇒ \(\widehat{xEF}\) =  180⁰ - \(\widehat{EFG}\) = 180⁰ - 120⁰ = 60⁰

\(\widehat{BEF}\) = \(\widehat{BEx}\) +  \(\widehat{xEF}\) = 49⁰ + 60⁰ = 109⁰ 

Kết luận: góc BEF là 109⁰

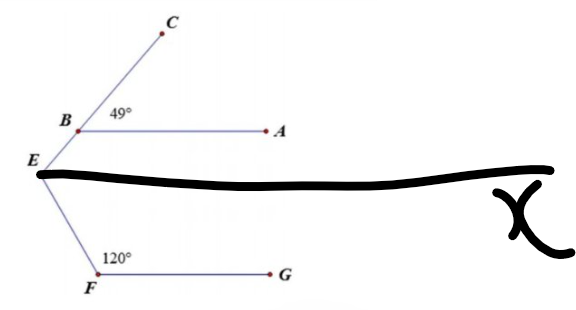
Kẻ Ex//AB(Ex và AB nằm trên cùng mặt phẳng bờ chứa tia BE)

Ta có: Ex//AB

AB//FG

Do đó: Ex//FG

Ex//AB

=>\(\widehat{BEx}=\widehat{CBA}\)(hai góc đồng vị)

=>\(\widehat{xEB}=49^0\)

Ta có: Ex//FG

=>\(\widehat{xEF}+\widehat{EFG}=180^0\)

=>\(\widehat{xEF}=180^0-120^0=60^0\)

\(\widehat{BEF}=\widehat{xEB}+\widehat{xEF}=49^0+60^0=109^0\)

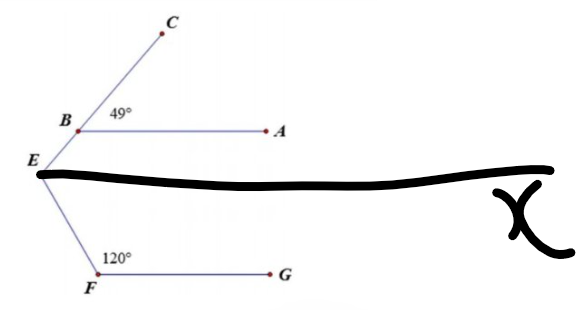
Kẻ Ex//AB(Ex và AB nằm trên cùng mặt phẳng bờ chứa tia BE)

Ta có: Ex//AB

AB//FG

Do đó: Ex//FG

Ex//AB

=>\(\widehat{BEx}=\widehat{CBA}\)(hai góc đồng vị)

=>\(\widehat{xEB}=49^0\)

Ta có: Ex//FG

=>\(\widehat{xEF}+\widehat{EFG}=180^0\)

=>\(\widehat{xEF}=180^0-120^0=60^0\)

\(\widehat{BEF}=\widehat{xEB}+\widehat{xEF}=49^0+60^0=109^0\)

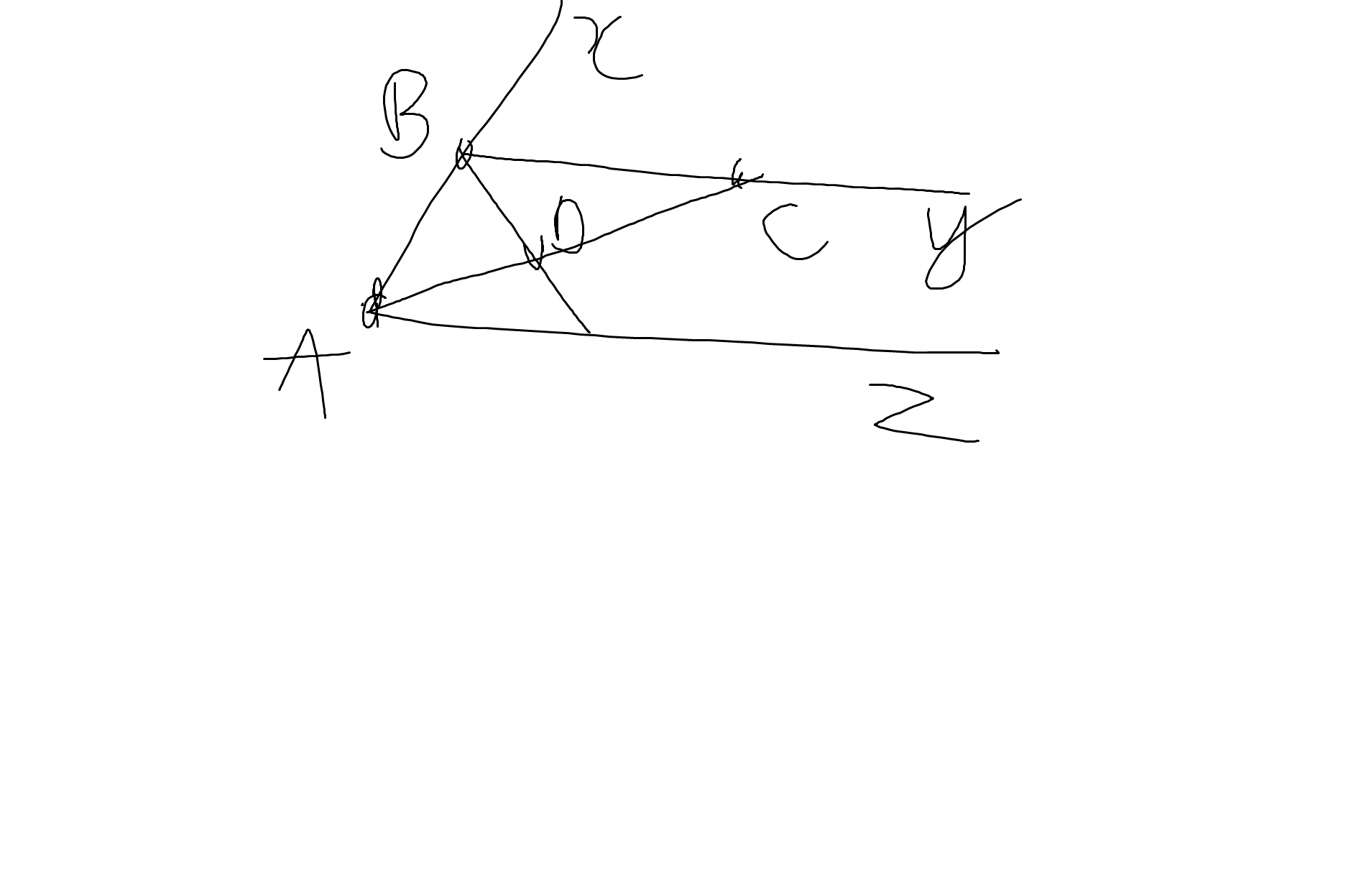
a: Ta có: \(\widehat{xBy}=\widehat{xAz}\left(=60^0\right)\)

mà hai góc này là hai góc ở vị trí đồng vị

nên By//Az

b: Ta có: \(\widehat{ABC}+\widehat{xBC}=180^0\)(hai góc kề bù)

=>\(\widehat{ABC}+60^0=180^0\)

=>\(\widehat{ABC}=120^0\)

AC là phân giác của góc zAB

=>\(\widehat{BAC}=\dfrac{\widehat{xAB}}{2}=30^0\)

Xét ΔBAC có \(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^0\)

=>\(\widehat{BCA}+120^0+30^0=180^0\)

=>\(\widehat{BCA}=30^0\)

c: Ta có: BD là phân giác của góc ABC

=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=60^0\)

Xét ΔDBA có \(\widehat{DBA}+\widehat{DAB}=60^0+30^0=90^0\)

nên ΔBDA vuông tại D

=>BD\(\perp\)AC

AE//BD

=>\(\widehat{BAE}+\widehat{ABD}=180^0\)(hai góc trong cùng phía)

=>\(\widehat{BAE}+90^0=180^0\)

=>\(\widehat{BAE}=90^0\)

Ta có: AE//BD

=>\(\widehat{AED}+\widehat{BDE}=180^0\)(hai góc trong cùng phía)

=>\(\widehat{BDE}+55^0=180^0\)

=>\(\widehat{BDE}=125^0\)

a: a\(\perp\)HK

b\(\perp\)HK

Do đó: a//b

b: Ta có: \(\widehat{BAH}+45^0=180^0\)

=>\(\widehat{BAH}=180^0-45^0=135^0\)

Ta có: a//b

=>\(\widehat{BAH}+\widehat{ABK}=180^0\)(hai góc trong cùng phía)

=>\(\widehat{ABK}+135^0=180^0\)

=>\(\widehat{ABK}=45^0\)