Áp dụng BĐT Cauchy Schwarz ta có:

\(\left(x^2+y^2+z^2\right)\left(y^2+z^2+x^2\right)\ge\left(xy+yz+xz\right)^2\)

\(\Leftrightarrow x^2+y^2+z^2\ge\left|xy+yz+xz\right|\ge xy+yz+xz\left(1\right)\)

Mặt khác:

\(\left(x+y+z\right)^2=x^2+y^2+z^2+2\left(xy+yz+xz\right)\)

\(\Leftrightarrow x^2+y^2+z^2=9-2\left(xy+yz+xz\right)\)

Kết hợp với \(\left(1\right)\Rightarrow9-2\left(xy+yz+xz\right)\ge xy+yz+xz\)

\(\Leftrightarrow3\left(xy+yz+xz\right)\le9\Leftrightarrow xy+yz+xz\le3\)

Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\frac{x}{y}=\frac{y}{z}=\frac{z}{x}\\x+y+z=3\end{cases}}\Leftrightarrow x=y=z=1\)

Vậy \(Max\) biểu thức là \(3\Leftrightarrow x=y=z=1\)

Với \(x,y,z\)ta có :

\(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2>=0\)

\(\Leftrightarrow2x^2+2y^2+2z^2-2xy-2yz-2xz\ge=0\)

\(x^2+y^2+z^2-xy-yz-zx\ge=0\)

\(\left(y+x+z\right)^2\ge=3\left(x+y+z\right)\)

\(\frac{\left[\left(x+y+z\right)^2\right]}{3}\ge=xy+zx+yz\)

\(\Rightarrow xy+yz+zx\le=3\)

Dấu \(=\)xảy ra khi \(x=y=z=1\)

cách này của lớp 8 nhé:

tự chứng minh BAC=1/2DAE

Mà MHB=1/2DAE

=> BAC=MHB

mà góc B chung của 2 tam giác BAC và MHB

=> tam giác BAC đồng dạng tam giác BHM (g.g)

=> \(\frac{AB}{BH}=\frac{BC}{BM}\Rightarrow\frac{AB}{BC}=\frac{BH}{BM}\)

Mà góc B chung của tam giác BHA và BMC

=> tam giác BHA đồng dạng tam giác BMC

=> BHA=BMC=90 độ => CM vuông góc AB

chứng minh tương tự => BN v góc

cách 2 (lớp 9)

giống như cách trên ta chứng minh được MHB=BAC

hay MHB=MAC

=> MAC+MHC=180

=> tứ giác AMHC nội tiếp

=> AMC=AHC=90

=> CM vuông góc AB

Bài khó đây bạn mà mình cũng chỉ đang học lớp 5 .

~~~ Chúc bạn học giỏi nha ~~~

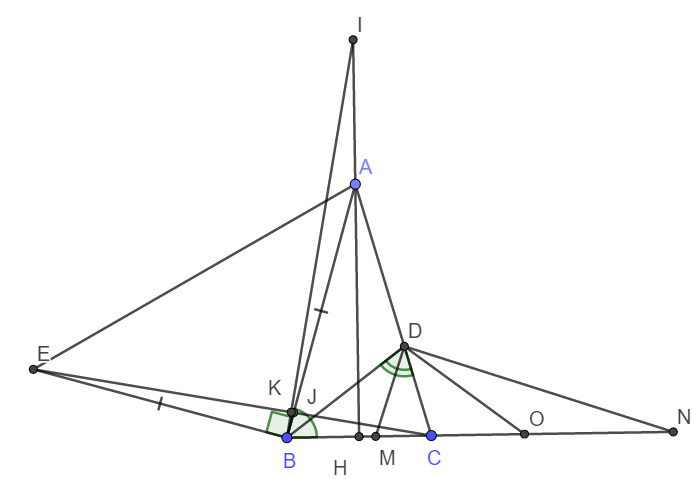
a)

+) Do tam giác ABC cân tại A nên trung tuyến AH đồng thời là đường caio.

Vậy nên \(\widehat{AHB}=90^o\)

Theo tính chất góc ngoài của tam giác, ta có:

\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)

Xét tam giác ABI và tam giác BEC có:

AI = BC (gt)

BA = EB (gt)

\(\widehat{IAB}=\widehat{CBE}\)  (cmt)

\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)

+) Gọi giao điểm của EC với AB và BI lần lượt là J và K.

Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)

Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)

Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)

b) Gọi O là trung điểm MN. Ta thấy DN và DM là phân giác của hai góc kề bù nên chúng vuông góc với nhau.

Vậy tam giác DMN vuông tại D. Khi đó ta có DO là trung tuyến ứng với cạnh huyền nên DO  =  MN/2

Vậy DO = OM = OM hay các tam giác DOM và DON cân tại O.

Ta có: \(\widehat{DOM}=180^o-2\widehat{DMO}=180^o-2\left(\widehat{MDB}+\widehat{MBD}\right)\)

\(=180^o-2.\widehat{MDB}-2.\widehat{MBD}=180^o-\widehat{BDC}-\widehat{ABC}\)

\(=180^o-\widehat{BDC}-\widehat{ACB}=\widehat{DBO}\)

Vậy tam giác DBO cân tại D hay DB = DO.

Vậy nên BD = MN/2.

xét tam giác BAI va CBE

be=ab

bc=ia

iab=ebc

=>tam giác BAI=tam giác CBE

Vai trò của p,q,r là như nhau nên giả sử như sau:p<q<r

Xét p=2, ta tìm được 3 số là:2;3;5(ko thỏa mãn)

Xét p=3,ta tìm được 3 số là:3;5;7(thỏa mãn)

Xét p>3

Bổ đề:Mọi số nguyên tố>3nên xem bình phương lên thì luôn chia 3 dư 1 thật vậy các số nguyên tố lớn hơn 3 nên có dạng:3k+1hoặc 3k+2

Nếu có dạng 3k+1,ta có: (3k+1)²=9k²+6k+1_1(mod3)

Nếu có dạng 3k+2 ,ta có:(3k+2)²=9k²+12k+4_1 (mod3)

Vậy nếu p>3 thì các số q,r>3 nên khi bình phương lên thì đều dư 1

==>p²+q²+r²=0(mod3)

Vậy ta có:(3,5,7)và các hoán vị

bạn lương đúng rồi

quá dễ 

=1

3 cái nha

không biết lớp 5 đây

49876

kick nha

49876