a) Do AD là tia phân giác của ∠BAC (gt)

⇒ ∠BAD = ∠CAD

Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét ∆ABD và ∆ACD có:

AB = AC (cmt)

∠BAD = ∠CAD (cmt)

AD là cạnh chung

⇒ ∆ABD = ∆ACD (c-g-c)

b) Do ∆ABD = ∆ACD (cmt)

⇒ ∠ADB = ∠ADC (hai góc tương ứng)

Mà ∠ADB + ∠ADC = 180⁰ (kề bù)

⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰

⇒ AD ⊥ BC (1)

Do ∆ABD = ∆ACD (cmt)

⇒ BD = CD (hai cạnh tương ứng)

⇒ D là trung điểm của BC (2)

Từ (1) và (2) ⇒ AD là đường trung trực của BC

c) Do ∠BAD = ∠CAD (cmt)

⇒ ∠MAD = ∠NAD

Xét ∆ADM và ∆ADN có:

AD là cạnh chung

∠MAD = ∠NAD (cmt)

AM = AN (gt)

⇒ ∆ADM = ∆ADN (c-g-c)

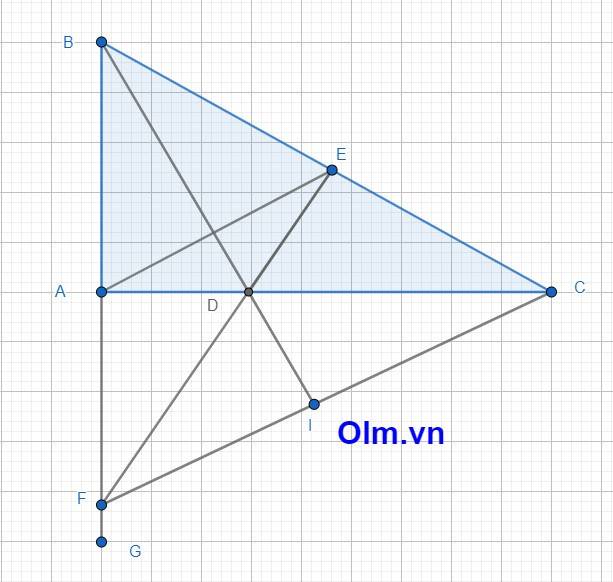
a; Xét tam giác ABD và tam giác EBD có:

 \(\widehat{ABD}\) = \(\widehat{EBD}\) (vì BD là phân giác góc ABC)

   AB = BE (gt)

Cạnh BD chung

⇒ \(\Delta\)ABD = \(\Delta\)EBD (c-g-c) 

⇒\(\widehat{BED}\) = \(\widehat{BAD}\) = 90⁰

⇒DE  \(\perp\) BC 

b; Xét tam giác BEF và tam giác ABC có:

\(\widehat{BAC}\)  = \(\widehat{BEF}\) = 90⁰

AB = BE (gt)

\(\widehat{ABE}\) chung

⇒ \(\Delta\)FBE = \(\Delta\)CBA (g-c-g)

⇒ BC = BF

BC = BE + EC = AB + AF

⇒ AF = EC

c; Xét tam giác BCF có BC = BF (cmt)

⇒ \(\Delta\)BCF cân tại B 

BD là phân giác của góc B ⇒ BD là trung tuyến tam giác BCF

⇒BD \(\equiv\) BI ⇒ B;D;I thẳng hằng (vì qua một đỉnh chỉ kẻ được một đường trung tuyến của tam giác)

d; \(\widehat{AEB}\) = \(\widehat{EAC}\) + \(\widehat{ECA}\) (góc ngoài của tam giác bằng hai góc trong không kề với nó)

 Xét tam giác ABE có: AB = BE (gt)

⇒ \(\Delta\)ABE cân tại B 

⇒ \(\widehat{BAE}\) = \(\widehat{AEB}\) = \(\widehat{EAC}\) + \(\widehat{ECA}\) (đpcm)

Ta có: \(-3x=5y\Rightarrow\dfrac{-3x}{15}=\dfrac{5y}{15}\Rightarrow\dfrac{x}{-5}=\dfrac{y}{3}\Rightarrow\dfrac{x}{35}=\dfrac{y}{-21}\)(1)

\(-2y=7z\Rightarrow\dfrac{-2y}{14}=\dfrac{7z}{14}\Rightarrow\dfrac{y}{-7}=\dfrac{z}{2}\Rightarrow\dfrac{y}{-21}=\dfrac{z}{6}\) (2) 

Từ (1) và (2) ta có: \(\dfrac{x}{35}=\dfrac{y}{-21}=\dfrac{z}{6}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{35}=\dfrac{y}{-21}=\dfrac{z}{6}=\dfrac{2x-3y+z}{2\cdot35-3\cdot-21+6}=\dfrac{42}{139}\) 

\(\Rightarrow\dfrac{x}{35}=\dfrac{42}{139}\Rightarrow x=\dfrac{1470}{139}\)

\(\Rightarrow\dfrac{y}{-21}=\dfrac{42}{139}\Rightarrow y=-\dfrac{882}{139}\)

\(\Rightarrow\dfrac{z}{6}=\dfrac{42}{139}\Rightarrow z=\dfrac{252}{139}\) 

giup mik vs

 Trong tam giác ABC có \(\widehat{B}< \widehat{C}\) nên \(AC< AB\) (quan hệ giữa góc và cạnh đối diện trong tam giác)

 Hơn nữa, vì AH là đường cao của tam giác ABC nên BH, CH lần lượt là hình chiếu của AB, AC trên đường thẳng BC. 

 \(\Rightarrow CH< BH\) (quan hệ đường xiên - hình chiếu)

 (Bạn xem lại đề bài nhé, mình nghĩ nó là \(BH>HC\) đó. Nhìn từ hình vẽ cũng có thể thấy. Ý thứ 2 cũng vậy, mình nghĩ là \(BD>DC\))

\(\left(x-1\right)^2=\left(x-1\right)^4\)

\(\Rightarrow\left(x-1\right)^4-\left(x-1\right)^2=0\)

\(\Rightarrow\left(x-1\right)^2\left[\left(x-1\right)^2-1\right]=0\) 

+) \(\left(x-1\right)^2=0\)

\(\Rightarrow x-1=0\)

\(\Rightarrow x=1\)

+) \(\left(x-1\right)^2-1=0\)

\(\Rightarrow\left(x-1\right)^2=1\)

\(\Rightarrow\left(x-1\right)^2=1^2\)

TH1: \(x-1=1\Rightarrow x=1+1=2\)

TH2: \(x-1=-1\Rightarrow x=-1+1=0\)

Vậy: \(x\in\left\{1;2;0\right\}\)

\(\left(x-1\right)^2=\left(x-1\right)^4\)

\(\Rightarrow\left(x-1\right)^2-\left(x-1\right)^4=0\)

\(\Rightarrow\left(x-1\right)^2\left[1-\left(x-1\right)^2\right]=0\)

\(\Rightarrow\left[{}\begin{matrix}\left(x-1\right)^2=0\\1-\left(x-1\right)^2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x-1=1\\x-1=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=2\\x=0\end{matrix}\right.\)

Vậy \(x\in\left\{1;2;0\right\}\)

for you

700

Minh tính sai có gì bạn thông cảm ạ 

280$ ạ

Đa thức \(2x^3-x^2+ax+b\)(*) chia hết cho \(x^2-1\) nên hai đa thức này có cùng nghiệm: 

Ta có: \(x^2-1=0\Leftrightarrow x=\pm1\)

+) Do `x=1` là nghiệm nên thay \(x=1\) vào (*) thì (*) sẽ bằng 0 ta có:

\(2\cdot1^3-1^2+a\cdot1+b=0\) 

\(\Leftrightarrow2-1+a+b=0\)

\(\Leftrightarrow a+b=-1\Leftrightarrow a=-1-b\) (1) 

+) Do \(x=-1\) là nghiệm nên thay \(x=-1\) vào (*) thì (*) sẽ bằng 0 ta có:

\(2\cdot\left(-1\right)^3-\left(-1\right)^2+a\cdot\left(-1\right)+b=0\)

\(\Leftrightarrow-2-1-a+b=0\)

\(\Leftrightarrow b-a=3\) (2)

Thay (1) vào (2) ta có:

\(b-a=3\Leftrightarrow b-\left(-1-b\right)=3\)

\(\Leftrightarrow b+1+b=3\)

\(\Leftrightarrow2b=2\)

\(\Leftrightarrow b=1\) 

\(\Rightarrow a=-1-1=-2\)

Vậy: ...