a) \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{100}}\)

\(2A=2\cdot\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{100}}\right)\)

\(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{101}}\)

\(2A-A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{99}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{100}}\)

\(A=1-\dfrac{1}{2^{100}}\)

b) \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2023\cdot2024}\)

\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\)

\(=1-\dfrac{1}{2024}\)

\(=\dfrac{2024}{2024}-\dfrac{1}{2024}\)

\(=\dfrac{2023}{2024}\)

cứu 

in free time nha

cứu

1 lớp học có số bạn nam bằng 3/4 số bạn nữ.Nếu thêm 2 bạn nam và 5 bạn nữ.Hỏi lớp đố cs bao nhiu hs

help

Khuyên lag không nên chê bai và vễ bậy lên các di tích 

Câu 3

a) Số bánh mì đã bán buổi sáng:

200 . 3/5 = 120 (bánh)

Số tiền bán được buổi sáng:

120 . 15000 = 1800000 (đồng)

b) Giá bánh mì buổi chiều:

15000 - 15000.20% = 12000 (đồng)

Số bánh mì bán buổi chiều:

200 - 120 = 80 (bánh)

Số tiền bán bánh buổi chiều:

80 . 12000 = 960000 (đồng)

Số tiền cả ngày bán bánh:

1800000 + 960000 = 2760000 (đồng)

Câu 4

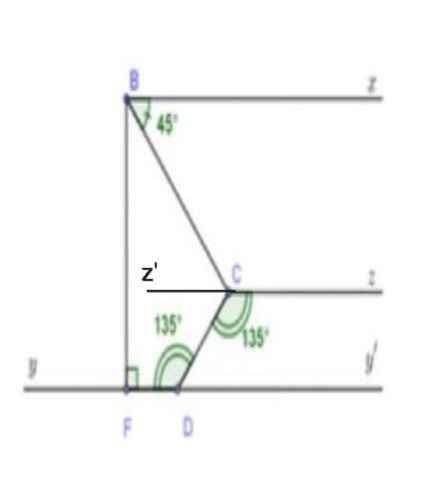  a) Ta có:

∠FDC = ∠DCz = 135⁰

Mà ∠FDC và ∠DCz là hai góc so le trong

⇒ Cz // Dy

b) Do Dy // Bx

Cz // Dy

⇒ Cz // Bx

Do Dy ⊥ BF

Dy // Bx

⇒ BF ⊥ Bx

⇒ ∠FBx = 90⁰

⇒ ∠FBC = ∠FBx - ∠CBx

= 90⁰ - 45⁰

= 45⁰

⇒ ∠FBC = ∠CBx = 45⁰

⇒ BC là tia phân giác của ∠FBx

c) Vẽ tia Cz' là tia đối của tia Cz

⇒ Cz' // Bx // Dy

Do Cz // Bx (cmt)

⇒ ∠BCz' = ∠CBx = 45⁰ (so le trong)

Ta có:

∠DCz' + ∠DCz = 180⁰ (kề bù)

⇒ ∠DCz' = 180⁰ - ∠DCz

= 180⁰ - 135⁰

= 45⁰

⇒ ∠DCz' = ∠BCz = 45⁰

⇒ Cz' là tia phân giác của ∠BCD

Do Ct là tia phân giác của ∠BCD

⇒ Ct ≡ Cz'

Mà Cz' // Dy (cmt)

⇒ Ct // Dy

Điểm trung bình môn Toán của An:

(7 + 8 + 9 + 10 + 8,5 . 2 + 9,5 . 3) : 9 ≈ 8,8