
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
a: \(k=\dfrac{y}{x}=\dfrac{3}{5}\)
b: \(\dfrac{y}{x}=\dfrac{3}{5}\)
=>\(y=\dfrac{3}{5}x\)
c: Thay x=-5 vào \(y=\dfrac{3}{5}x\), ta được:
\(y=\dfrac{3}{5}\cdot\left(-5\right)=-3\)
Thay x=15 vào \(y=\dfrac{3}{5}x\), ta được:
\(y=\dfrac{3}{5}\cdot15=9\)
Câu 4: Gọi khối lượng giấy vụn ba chi đội 7A,7B,7C thu được lần lượt là a(kg),b(kg),c(kg)
(Điều kiện:a>0; b>0; c>0)
Khối lượng giấy vụn của ba đội thu được lần lượt tỉ lệ với 9;7;8
=>\(\dfrac{a}{9}=\dfrac{b}{7}=\dfrac{c}{8}\)
Tổng khối lượng là 120kg nên a+b+c=120
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{9}=\dfrac{b}{7}=\dfrac{c}{8}=\dfrac{a+b+c}{9+7+8}=\dfrac{120}{24}=5\)
=>\(a=5\cdot9=45;b=7\cdot5=35;c=8\cdot5=40\)
vậy: Gọi khối lượng giấy vụn ba chi đội 7A,7B,7C thu được lần lượt là 45(kg),35(kg),40(kg)

a: Ta có: mn//xy
=>\(\widehat{mAB}=\widehat{ABy}\)(hai góc so le trong)
=>\(\widehat{mAB}=60^0\)
b:
Ta có: \(\widehat{yBc}+\widehat{yBA}=180^0\)(hai góc kề bù)
=>\(\widehat{yBc}=180^0-60^0=120^0\)
Bz là phân giác của góc yBc
=>\(\widehat{yBz}=\widehat{cBz}=\dfrac{\widehat{yBc}}{2}=\dfrac{120^0}{2}=60^0\)
Ta có: \(\widehat{nAB}+\widehat{mAB}=180^0\)(hai góc kề bù)
=>\(\widehat{nAB}=180^0-60^0=120^0\)
At là phân giác của góc nAB
=>\(\widehat{nAt}=\widehat{tAB}=\dfrac{\widehat{nAB}}{2}=\dfrac{120^0}{2}=60^0\)
Ta có: \(\widehat{ABz}=\widehat{ABy}+\widehat{yBz}=60^0+60^0=120^0\)
Ta có: \(\widehat{ABz}+\widehat{BAt}=120^0+60^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên At//Bz

Ta có: \(\left(x-3\right)\left(x-1\right)-x\left(2-x\right)=0\)
=>\(x^2-4x+3-2x+x^2=0\)
=>\(2x^2-6x+3=0\)
=>\(x^2-3x+\dfrac{3}{2}=0\)
=>\(x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{9}{4}+\dfrac{3}{2}=0\)
=>\(\left(x-\dfrac{3}{2}\right)^2-\dfrac{3}{4}=0\)
=>\(\left(x-\dfrac{3}{2}\right)^2=\dfrac{3}{4}\)
=>\(\left[{}\begin{matrix}x-\dfrac{3}{2}=\dfrac{\sqrt{3}}{2}\\x-\dfrac{3}{2}=-\dfrac{\sqrt{3}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{3}}{2}\\x=\dfrac{3-\sqrt{3}}{2}\end{matrix}\right.\)

Bài 1:
B = \(x^2\) - 2\(xy\) + 2y2
Thay \(x=13\) và y = 3 vào B ta được
B = 132 - 2.13.3 + 2.32
B = 169 - 26.3 + 2.9
B = 169 - 78 + 18
B = 91 + 18
B = 109

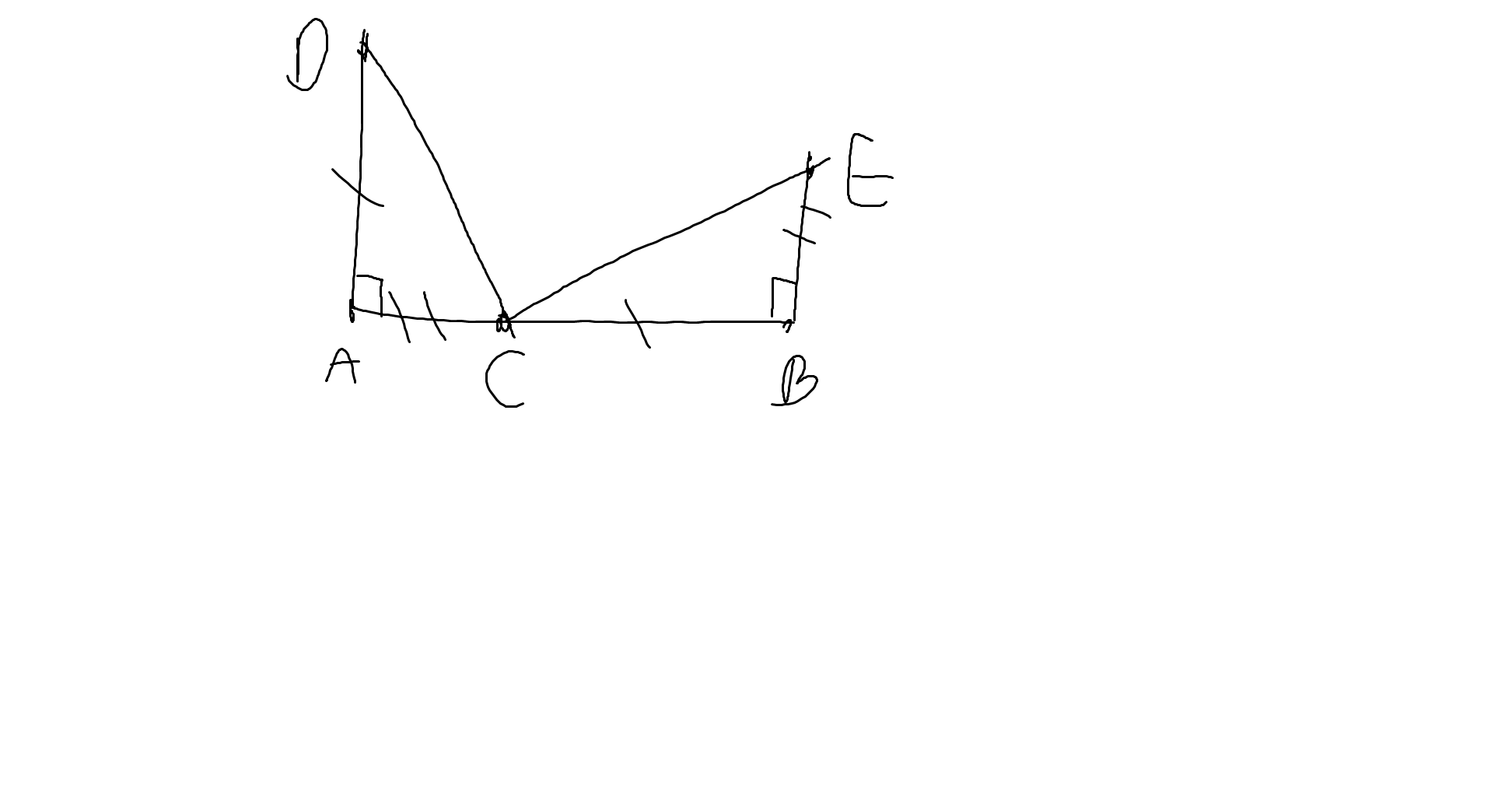
a: Xét ΔDAC vuông tại A và ΔCBE vuông tại B có
DA=CB
AC=BE
Do đó: ΔDAC=ΔCBE
b: ΔDAC=ΔCBE
=>\(\widehat{DCA}=\widehat{CEB}\)
=>\(\widehat{DCA}+\widehat{ECB}=90^0\)
Ta có: \(\widehat{DCA}+\widehat{ECB}+\widehat{DCE}=180^0\)
=>\(\widehat{DCE}+90^0=180^0\)
=>\(\widehat{DCE}=90^0\)
=>CD\(\perp\)CE

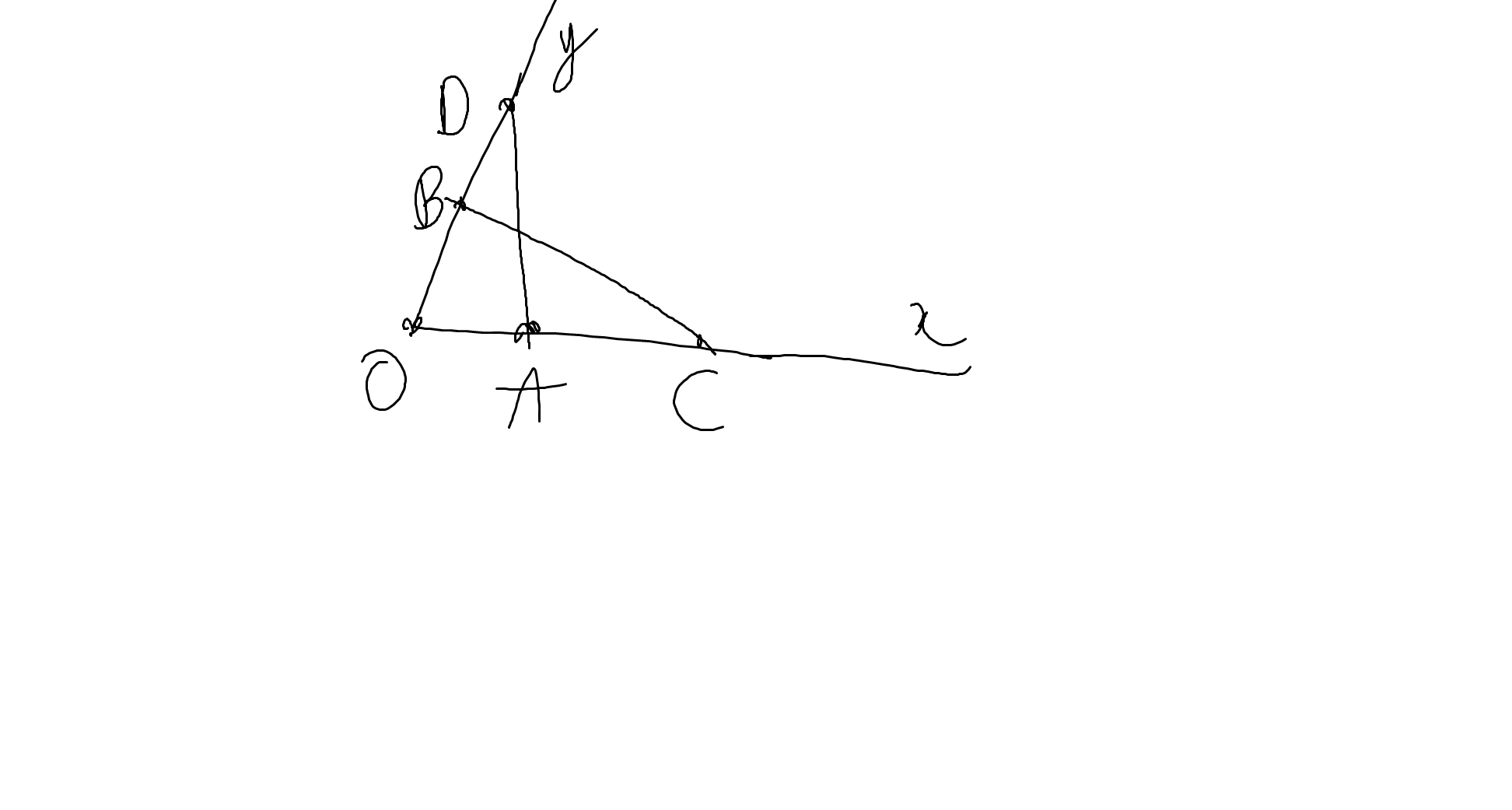
Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
=>AD=BC

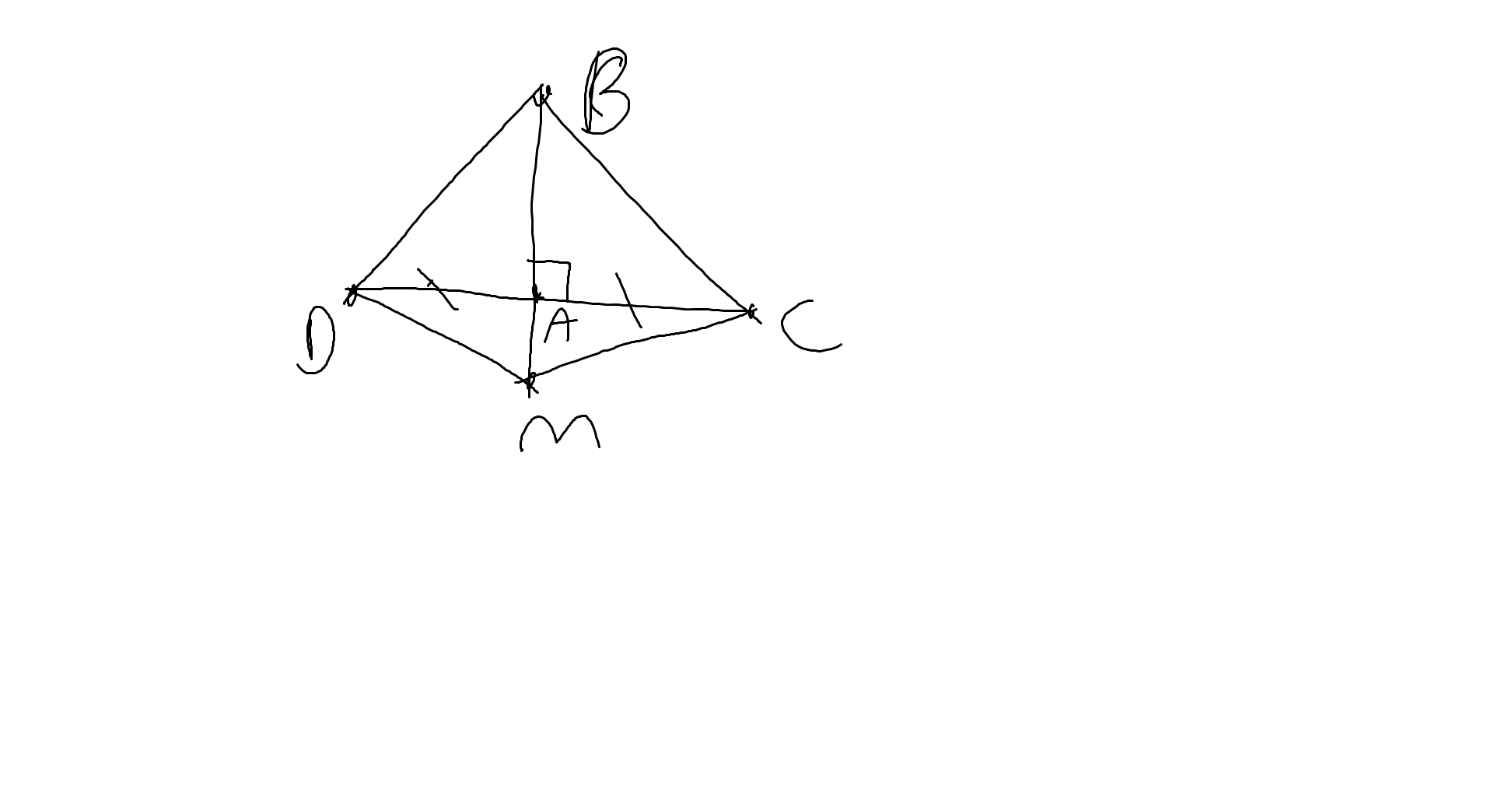
a: Xét ΔABD vuông tại A và ΔABC vuông tại A có
AB chung
AD=AC
Do đó: ΔABD=ΔABC
b: ΔABD=ΔABC
=>BD=BC
ΔABD=ΔABC
=>\(\widehat{ABD}=\widehat{ABC}\)
=>\(\widehat{MBC}=\widehat{MBD}\)
Xét ΔMBC và ΔMBD có
MB chung
\(\widehat{MBC}=\widehat{MBD}\)
BC=BD
Do đó: ΔMBC=ΔMBD

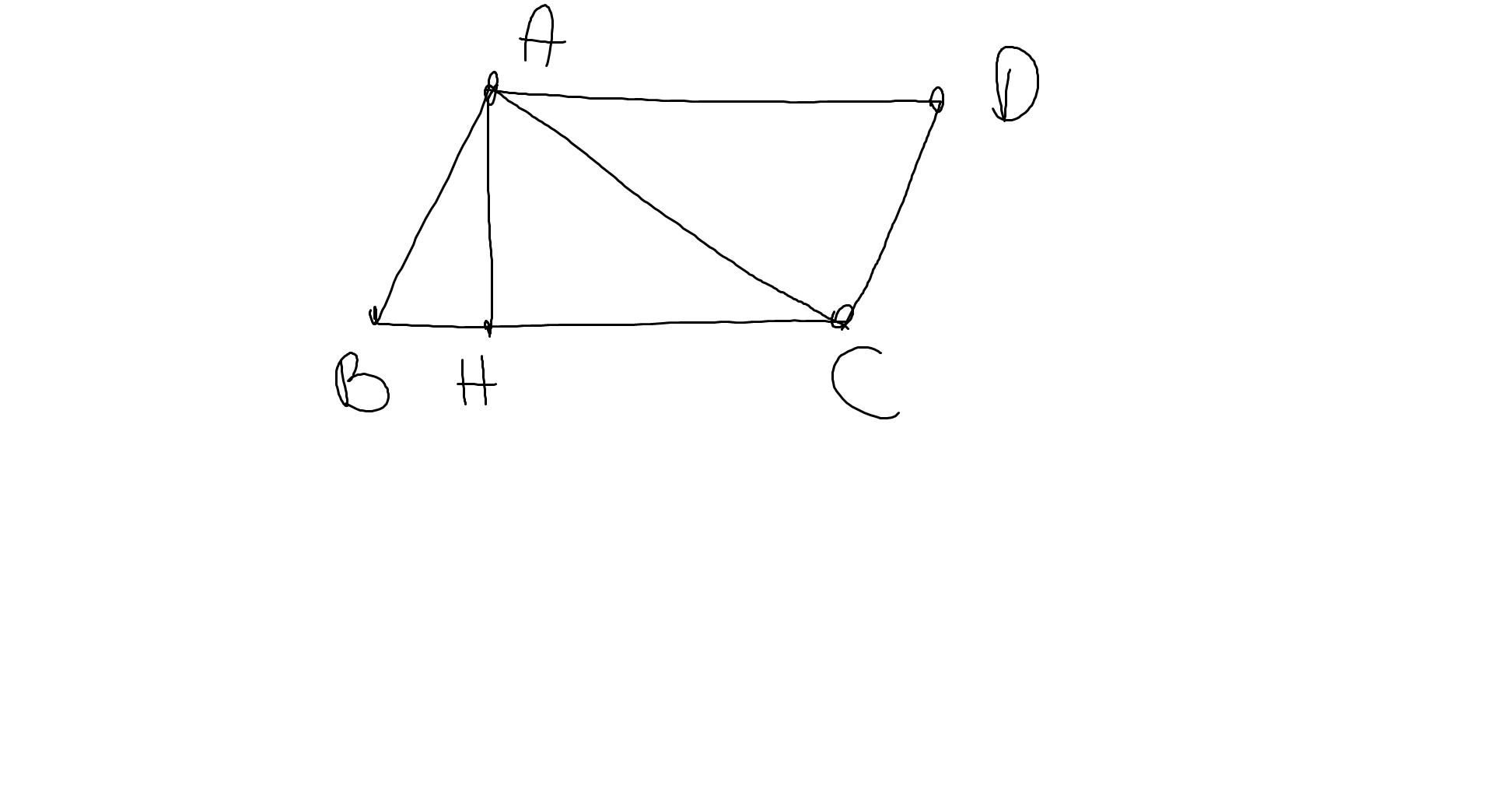
a: Xét ΔABC và ΔCDA có
AB=CD
AC chung
BC=DA
Do đó: ΔABC=ΔCDA
=>\(\widehat{BAC}=\widehat{DCA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
b: ΔABC=ΔCDA
=>\(\widehat{ACB}=\widehat{DAC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
mà AH\(\perp\)BC
nên AH\(\perp\)AD

a: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//EB
b: Xét ΔMAI và ΔMEK có
MA=ME
\(\widehat{MAI}=\widehat{MEK}\)(cmt)
AI=EK
Do đó: ΔMAI=ΔMEK
=>\(\widehat{AMI}=\widehat{EMK}\)
=>\(\widehat{EMK}+\widehat{EMI}=180^0\)
=>I,M,K thẳng hàng







Ta có: 1; 2; 3; 4..; 1999; 2022
Dãy số trên từ 1 đến 1999 là dãy số cách đều với khoảng cách là:
2 - 1 = 1
Tại sao 2022 lại không theo quy luật đó
2022 - 1999 = 2
Đề bài em chép đã đúng chưa?