573 \(\times\) (894 - 884)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 15:
Đây là toán nâng cao chuyên đề bài toán tính tuổi, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng sơ đồ đoạn thẳng như sau:
Giải:
Hiệu số tuổi hai cô cháu bằng: (3 - 1): 1 = \(\frac21\) (tuổi Linh hiện nay)
Coi tuổi Linh hiện nay là 1 phần
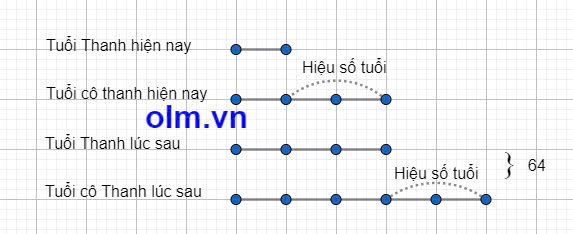
ta có sơ đồ:
Theo sơ đồ ta có:
Tuổi Linh hiện nay là: 64:(3 + 2 + 3) = 8 (tuổi)
Tuổi cô Thanh hiện nay là: 8 : \(\frac13\) = 24(tuổi)
Đáp số:
Tuổi Linh hiện nay là: 8 tuổi.
Tuổi cô Thanh hiện nay là 24 tuổi

Olm chào em đây là toán nâng cao chuyên đề bài toán về tính tuổi, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải dạng này bằng phương pháp toán hai tỉ số trong đó có một đại lượng không đổi.
Giải:
Vì mỗi năm mỗi người thêm một tuổi nên hiệu số tuổi hai mẹ con luôn không đổi theo thời gian.
Hiện nay tuổi con là:
1 :(4 - 1) = \(\frac13\) (hiệu số tuổi hai mẹ con)
6,4 = \(\frac{32}{5}\)
Tuổi con bốn năm trước là:
5:(32 - 5) = \(\frac{5}{27}\) (hiệu số tuổi hai mẹ con)
4 tuổi ứng với phân số là:
\(\frac13-\frac{5}{27}\) = \(\frac{4}{27}\) (hiệu số tuổi hai mẹ con)
Hiệu số tuổi hai mẹ con là:
4 : \(\frac{4}{27}\) = 27 (tuổi)
Vậy mẹ sinh con năm mẹ 27 tuổi
Đáp số: 27 tuổi

Đây là toán nâng cao chuyên đề toán tổng hiệu ẩn hiệu, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Vì giữa hai số chẵn có 5 số chẵn nên số số chẵn là: 2 + 5 = 7(số)
Hiệu hai số là: 2 x (7 - 1) = 12
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số chẵn bé là: (240 - 12) : 2 = 114
Số chẵn lớn là: 114 + 12 = 126
Đáp số: Số chẵn bé là 114; số chẵn lớn là 126

Olm chào em, đây là toán nâng cao chuyên đề số thập phân, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải dạng này như sau:
Giải:
Vì dịch dấu phẩy của một số thập phân ban đầu sang trái một hàng thì được số mới nên số mới bằng:
1 : 10 = \(\frac{1}{10}\)(số ban đầu)
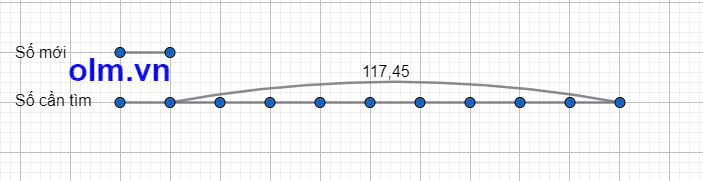
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số thập phân cần tìm là:
117,45:(10 - 1) x 10 = 130,5
Đáp số: 130,5

Olm chào em, đây là toán nâng cao chuyên đề số thập phân, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải dạng này như sau:
Giải:
Vì dịch dấu phẩy của một số thập phân ban đầu sang trái một hàng thì được số mới nên số mới bằng:
1 : 10 = \(\frac{1}{10}\)(số ban đầu)
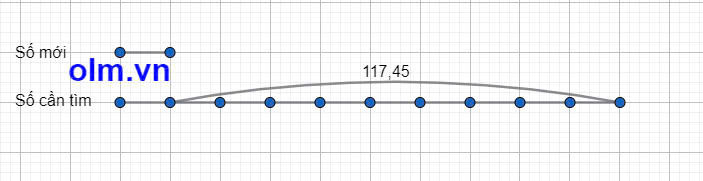
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số thập phân cần tìm là:
117,45:(10 - 1) x 10 = 130,5
Đáp số: 130,5

Câu 2: Năm nay tuổi bố gấp 5 lần tuổi con
=>Tuổi bố=5 lần tuổi con
21 năm sau, tuổi bố gấp đôi tuổi con
=>tuổi bố+21=2(tuổi con+21)
=>5 lần tuổi con+21=2 lần tuổi con+42
=>3 lần tuổi con là 42-21=21
Tuổi con hiện nay là 21:3=7(tuổi)
Tuổi bố hiện nay là 7x5=35(tuổi)
Câu 3: Năm nay, tuổi Nam bằng 1/4 tuổi ông nội
=>Tuổi ông=4 lần tuổi Nam
6 năm trước, tuổi Nam bằng 2/11 lần tuổi của ông Nội
=>tuổi Nam-6=2/11(tuổi ông-6)
=>tuổi Nam-6=2/11(4 lần tuổi Nam-6)
=>tuổi Nam-6=8/11 tuổi Nam-12/11
=>3/11 tuổi Nam là \(6-\dfrac{12}{11}=\dfrac{66}{11}-\dfrac{12}{11}=\dfrac{54}{11}\)
Tuổi Nam hiện nay là \(\dfrac{54}{11}:\dfrac{3}{11}=18\left(tuổi\right)\)
Tuổi ông hiện nay là 18x4=72(tuổi)
Câu 4: 8 năm về trước, tuổi chú gấp 6 lần tuổi cháu
=>Tuổi chú -8=6 x (tuổi cháu-8)
=>tuổi chú -8=6x(3/8 tuổi chú-8)
=>tuổi chú-8=9/4 lần tuổi chú-48
=>5/4 lần tuổi chú là 48-8=40
Tuổi chú là \(40:\dfrac{5}{4}=40\times\dfrac{4}{5}=32\left(tuổi\right)\)
Tuổi cháu hiện nay là \(32\times\dfrac{3}{8}=12\left(tuổi\right)\)
Câu 5:
Sau đây 10 năm thì tuổi con bằng 7/19 tuổi mẹ
=>Tuổi con+10 =7/19(tuổi mẹ+10)
=>Tuổi con+10=7/19(7x tuổi con+10)
=>Tuổi con+10=49/19 lần tuổi con+70/19
=>19 lần tuổi con+190=49 lần tuổi con+70
=>30 lần tuổi con là 190-70=120
Tuổi con hiện nay là 120:30=4(tuổi)
Tuổi mẹ hiện nay là 7x4=28(tuổi)
Bài 2:
Giải:
Vì mỗi năm mỗi người thêm một tuổi nên hiệu số tuổi hai bố con không đổi theo thời gian.
Tuổi con hiện nay là:
1 : (5 - 1) = \(\frac14\) (tuổi hai bố con)
Tuổi con hai mươi mốt năm sau là:
1 :(2 - 1) = \(\frac11\) (hiệu số tuổi hai bố con)
21 tuổi ứng với phân số là:
\(\frac11-\frac14=\frac34\) (hiệu số tuổi hai bố con)
Hiệu số tuổi hai bố con là:
21 : \(\frac34=28\) (tuổi)
Tuổi con hiện nay là:
28 x \(\frac14=7\) (tuổi)
Tuổi bố hiện nay là: 7 + 28 = 35(tuổi)
Đáp số: tuổi bố hiện nay là 35 tuổi, tuổi con hiện nay là 7 tuổi

Xu với coin dùng để đổi những thứ vật dụng hay áo quần chẳng hạn
Xu/ Coin (1 coin = 10 xu) dùng để đổi các quà hay thẻ điện thoại trong shop của olm
- Bạn có thể đổi quả ở đây nhé !
https://shop.olm.vn/doi-qua

Thời gian Như làm mỗi con hạc giấy là:
\(20,4:4=5,1\) (phút) = 5 phút 6 giây
Đáp số: 5 phút 6 giây

Giải:
Số có hai chữ số có dạng: \(\overline{ab}\)
Viết thêm chữ số 0 vào giữa hai chữ số của số đó ta được số mới là: \(\overline{a0b}\)
Theo bài ra ta có:
\(\overline{a0b}\) = 6 x \(\overline{ab}\)
100a + b = 60a + b
100a + b - 60a - 6b = 0
(100a - 60a) - (6b - b) = 0
40a - 5b = 0
8a - b = 0
8a = b
b ≤ 9 ⇒ 8a ≤ 9 ⇒ a ≤ 9 : 8 ⇒ a < 2 ⇒ a = 0; 1
Vì a không thể bằng không nên a = 1, b = 8a = 8.1 = 8
Vậy số cần tìm là 18






573x(894-884)
=573x10
=5730
573x10
=5730