SOS nhanh lên 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


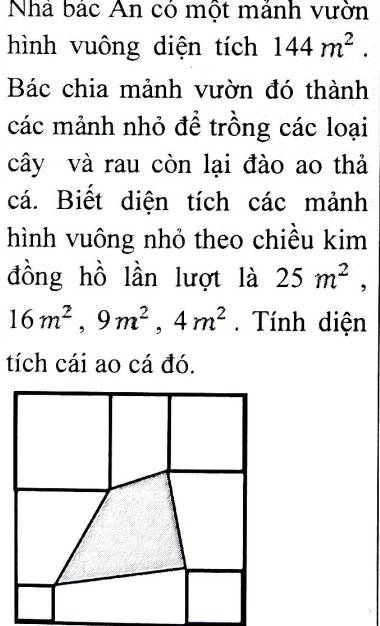
Ta đánh số các hình như hình minh họa khi đó ta có:
Vì 144 = 12 x 12
Vậy cạnh hình vuông mảnh đất là 12 m
25 = 5 x 5; 16 = 4 x 4 ; 9 = 3 x 3; 4 = 2 x 2
Vậy cạnh hình vuông của các mảnh đất nhỏ theo thứ tự chiều kim đồng hồ lần lượt là:
5m; 4m; 3m; 2m
Chiều cao của hình thang thứ nhất:
12 - 5 - 4 = 3 (m)
Chiều cao của hình thang thứ hai là:
12 - 4 - 3 = 5(m)
Chiều cao của hình thang thứ tư là:
12 - 3 - 2 = 7 (m)
Diện tích hình thang thứ nhất là:
(5 + 4) x 3 : 2 = 13,5 (m2)
Diện tích hình thang thứ hai là:
(4 + 3) x 5 : 2 = 17,5 (m2)
Diện tích hình thang thứ ba là:
(3 + 2) x 7: 2 = 17,5 (m2)
Diện tích hình thang thứ tư là:
(2 + 5) x 5 : 2 = 17,5 (m2)
Diện tích ao cá là:
144 - 13,5 - 17,5 - 17,5 - 17,5 = 78 (m2)
Đáp số: 78 m2

\(3n+5⋮n-3\)
=>\(3n-9+14⋮n-3\)
=>\(14⋮n-3\)
=>\(n-3\in\left\{1;-1;2;-2;7;-7;14;-14\right\}\)
=>\(n\in\left\{4;2;5;1;10;-4;17;-11\right\}\)
mà n>=0
nên \(n\in\left\{4;2;5;1;10;17\right\}\)
(3n + 5) ⋮ (n - 3) đk n \(\in\) N
3(n - 3) + 14 ⋮ n - 3
14 ⋮ n - 3
n - 3 \(\in\) Ư(14) = {-14; -7; -2; -1; 1; 2; 7; 14}
n \(\in\) {-11; -4; 1; 2; 4; 5; 10; 17}
Vì n \(\in\) N nên n \(\in\) { 1; 2; 4; 5; 10; 17}

1: \(\left(2x+1\right)^2-2\left(2x+1\right)\left(3-x\right)+\left(x-3\right)^2\)
\(=\left(2x+1\right)^2+2\left(2x+1\right)\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(2x+1+x-3\right)^2=\left(3x-2\right)^2=9x^2-12x+4\)
2: \(\left(x-1\right)^3-\left(x+1\right)\left(x^2-x+1\right)-\left(1-3x\right)\left(1+3x\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+1\right)-\left(1-9x^2\right)\)
\(=x^3-3x^2+3x-1-x^3-1-1+9x^2\)
\(=6x^2+3x-3\)
3: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x-1\right)\left(x+1\right)+3x\)
\(=x^3+8-x\left(x^2-1\right)+3x\)
\(=x^3+8-x^3+x+3x=4x+8\)
4: \(\left(3x-2\right)^2-3\left(x-4\right)\left(x+4\right)+\left(x-3\right)^2-\left(x+1\right)\left(x^2-x+1\right)\)
\(=9x^2-12x+4-3\left(x^2-16\right)+x^2-6x+9-\left(x^3+1\right)\)
\(=10x^2-18x+13-3x^2+48-x^3-1\)
\(=-x^3+7x^2-18x+12\)
5: \(\left(x+1\right)^2-\left(x-1\right)^2-3\left(x-3\right)\left(x+3\right)\)
\(=x^2+2x+1-x^2+2x-1-3\left(x^2-9\right)\)
\(=4x-3x^2+27\)
6: \(\left(x-1\right)^3-x\left(x-2\right)^2+x-1\)
\(=x^3-3x^2+3x-1-x\left(x^2-4x+4\right)+x-1\)
\(=x^3-3x^2+4x-2-x^3+4x^2-4x\)
\(=x^2-2\)
7: \(\left(x+2\right)^3-x^2\left(x+6\right)-8\)
\(=x^3+6x^2+12x+8-x^3-6x^2-8\)
=12x
8: \(\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)
\(=\left(x^3+3x^2y+3xy^2+y^3\right)-\left(x^3-3x^2y+3xy^2-y^3\right)-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)
\(=6x^2y\)
9: \(\left(x-1\right)^3-\left(x+1\right)^3+6\left(x-1\right)\left(x+1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6\left(x^2-1\right)\)
\(=-6x^2-2+6x^2-6=-8\)
10: \(4x\left(3x-5\right)-2\left(4x+1\right)-x-7\)
\(=12x^2-20x-8x-2-x-7\)
\(=12x^2-29x-9\)
11: \(\left(3x+1\right)^2-2\left(3x+1\right)\left(5x+5\right)+\left(5x+5\right)^2\)
\(=\left(5x+5-3x-1\right)^2\)
\(=\left(2x+4\right)^2=4x^2+16x+16\)
12: \(\left(2x+3\right)^2+\left(2x+3\right)\left(2x-6\right)+\left(x-3\right)^2\)
\(=\left(2x+3\right)^2+2\cdot\left(2x+3\right)\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(2x+3+x-3\right)^2=\left(3x\right)^2=9x^2\)
13: \(\left(x^2-2x+4\right)\left(x+2\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)
\(=x^3+8-x^3-3x^2-3x-1+3\left(x^2-1\right)\)
\(=-3x^2-3x+7+3x^2-3=-3x+4\)
14: \(\left(x-2\right)^2+2\left(x-2\right)\left(2x+2\right)+4\left(x+1\right)^2\)
\(=\left(x-2\right)^2+2\left(x-2\right)\left(2x+2\right)+\left(2x+2\right)^2\)
\(=\left(x-2+2x+2\right)^2=\left(3x\right)^2=9x^2\)

Lời giải:
Áp dụng BĐT Cô-si:
$\frac{x^2+y^2}{4}+\frac{1}{x^2+y^2}\geq 2\sqrt{\frac{x^2+y^2}{4}.\frac{1}{x^2+y^2}}=1$
Áp dụng BĐT Bunhiacopxky:
$\frac{3(x^2+y^2)}{4}=\frac{3(1+1)(x^2+y^2)}{8}\geq \frac{3(x+y)^2}{8}=\frac{3.2^2}{8}=\frac{3}{2}$
$\Rightarrow B\geq 1+\frac{3}{2}=\frac{5}{2}$
Vậy $B_{\min}=\frac{5}{2}$
Giá trị này đạt tại $x=y=1$

\(3\left(\dfrac{1}{5}-x\right)=-\dfrac{9}{5}\)
⇔\(\left(\dfrac{1}{5}-x\right)=-\dfrac{9}{5}:3\)
⇔\(\left(\dfrac{1}{5}-x\right)=-\dfrac{9}{5}.\dfrac{1}{3}\)
⇔\(\left(\dfrac{1}{5}-x\right)=-\dfrac{3}{5}\)
⇔\(x=\dfrac{1}{5}-\left(-\dfrac{3}{5}\right)\)
⇔\(x=\dfrac{1}{5}+\dfrac{3}{5}\)
⇔\(x=\dfrac{4}{5}\)
Vậy \(x=\dfrac{4}{5}\)


12,6 × (y - 2) - y × 5,6 = 16,8
12,6 × y - 25,2 - y × 5,6 = 16,8
y × (12,6 - 5,6) = 16,8 + 25,2
y × 7 = 42
y = 42 : 7
y = 6

Số chữ số dùng để đánh số các số chẵn có 1 chữ số: 4 (chữ số)
Từ 10 đến 98 có số các số chẵn là:
(98 - 10) : 2 + 1 = 45 (số)
Số các chữ số dùng để đánh số các số chẵn từ 10 đến 98 là:
45 . 2 = 90 (chữ số)
Từ 100 đến 284 có số các số chẵn là:
(284 - 100) : 2 + 1 = 93 (số)
Số chữ số dùng để đánh số các số chẵn từ 100 đến 284 là:
93 . 3 = 279 (chữ số)
Số chữ số đã dùng để đánh số nhà chẵn:
279 + 90 + 4 = 373 (chữ số)
 SOS cần gấp
SOS cần gấp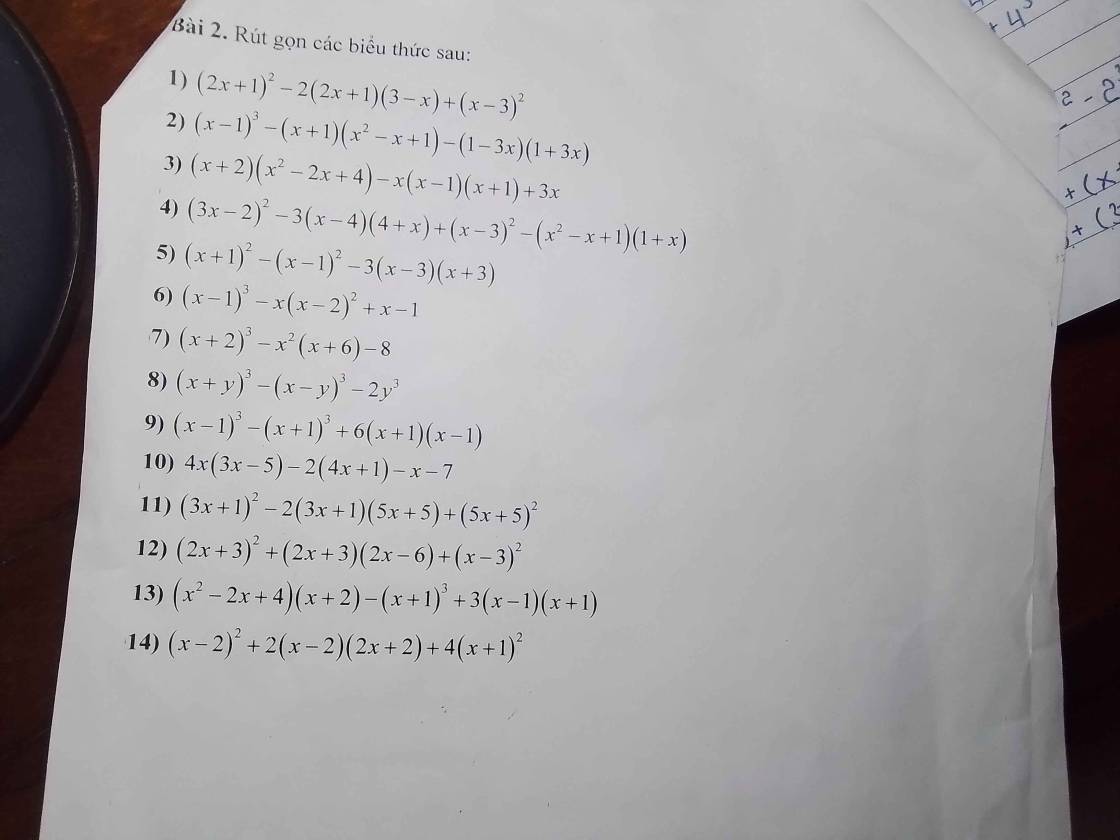

2 lần số trận thắng là: \(\dfrac{1800000}{200000}+15=24\)
=>Số trận thắng là 24:2=12(trận)
Giả sử tất cả các trận đều thắng thì số tiền thưởng là
200 000 . 15 = 3000 000 (đồng)
Giả sử thay một trận thắng bằng 1 trận thua thì số tiền mất đi là
200 000 + 200 000 = 400 000 (đồng)
Số trận thua là
(3000 000 - 1800 000) : 400 000 = 3 (trận)
Vậy đội đó thắng số trận là
15 -3 = 12 (trận)
Đáp số ....