2020 mũ trừ 1 chia 2020 mũ 2 cộng 2021
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x\ne2\)
\(P=\dfrac{x^4-16}{x^4-4x^3+8x^2-16x+16}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)\left(x^2+4\right)}{x^4+4x^2-4x^3-16x+4x^2+16}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)\left(x^2+4\right)}{x^2\left(x^2+4\right)-4x\left(x^2+4\right)+4\left(x^2+4\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x^2-4x+4}=\dfrac{x+2}{x-2}\)
Để P nguyên thì \(x+2⋮x-2\)
=>\(x-2+4⋮x-2\)
=>\(4⋮x-2\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)

Khối lượng 90 thùng na dai là:
90x5=450(kg)
Khối lượng hàng xe phải chở là 300+450=750(kg)>700kg
=>Xe đó không chở thêm được 90 thùng na dai

A B C a b c H K
a/ Dựng \(AH\perp BC\left(H\in BC\right)\)
Xét tg vuông ACH có
\(\cos C=\dfrac{CH}{AC}=\dfrac{CH}{b}\Rightarrow CH=b\cos C\)
Xét tg vuông ABH có
\(\cos B=\dfrac{BH}{AB}=\dfrac{BH}{c}\Rightarrow BH=c\cos B\)
\(\Rightarrow CH+BH=BC=a=b\cos C+c\cos B\)
b/
Đặt \(\widehat{BAH}=\alpha;\widehat{CAH}=\beta\)
\(\Rightarrow\cos A=\cos\left(\alpha+\beta\right)=\cos\alpha\cos\beta-\sin\alpha\sin\beta=\)
\(=\dfrac{AH}{c}.\dfrac{AH}{b}-\dfrac{BH}{c}.\dfrac{CH}{b}=\dfrac{AH^2-BH.CH}{bc}=\)
\(=\dfrac{2AH^2-2BH.CH}{2bc}=\dfrac{c^2-BH^2+b^2-CH^2-2BH.CH}{2bc}=\)
\(=\dfrac{b^2+c^2-\left(BH+CH\right)^2}{2bc}=\dfrac{b^2+c^2-a^2}{2bc}\)

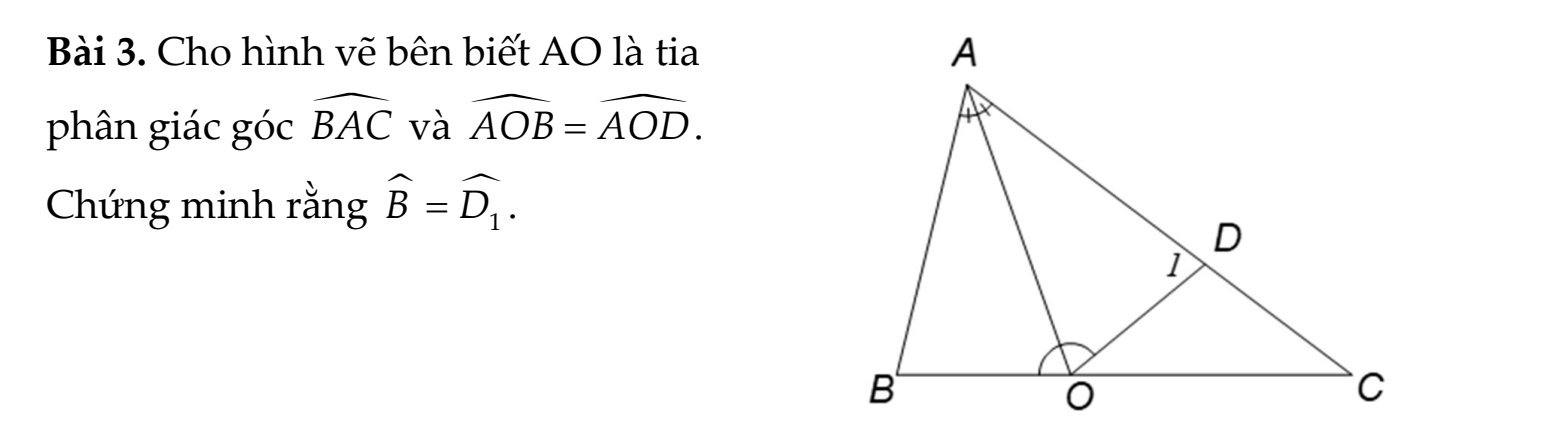
Xét 2 ΔABO và ΔADO ta có:
\(\widehat{BAO}=\widehat{DAO}\) (AD là phân giác của góc BAC)
\(OA\) chung
\(\widehat{AOB}=\widehat{AOD}\left(gt\right)\)
\(=>\Delta ABO=\Delta ADO\left(g.c.g\right)\)
\(=>\widehat{B}=\widehat{D_1}\) (hai góc tương ứng)

ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=100^0\)
AD là phân giác góc ngoài tại đỉnh A
=>\(\widehat{CAD}=\dfrac{180^0-\widehat{BAC}}{2}=40^0\)
=>\(\widehat{CAD}=\widehat{ACB}\left(=40^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC

Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(2\cdot\left(\widehat{OBC}+\widehat{OCB}\right)=90^0\)
=>\(\widehat{OBC}+\widehat{OCB}=45^0\)
Xét ΔOBC có \(\widehat{BOC}+\widehat{OBC}+\widehat{OCB}=180^0\)
=>\(\widehat{BOC}+45^0=180^0\)
=>\(\widehat{BOC}=135^0\)

\(\widehat{A}=180^o-\widehat{B}-\widehat{C}=180^o-40^o-40^o=100^o\)
=> \(\widehat{A_{ngoai}}=180^o-100^o=80^o\)
=> \(\widehat{DAB}=\dfrac{1}{2}\widehat{A_{ngoai}}=\dfrac{1}{2}\cdot80^o=40^o\)
Ta có: \(\widehat{DAB}=\widehat{ABC}\left(=40^o\right)\)
Mà 2 góc này ở vị trí so le trong
=> AD//BC

\(60=2^2.3.5\\ 63=3^2.7\\ \Rightarrow BCNN\left(60;63\right)=2^2.3^2.5.7=1260\)



Sửa đề: \(\dfrac{2020^3-1}{2020^2+2021}\)
\(=\dfrac{\left(2020-1\right)\left(2020^2+2020+1\right)}{2020^2+2020+1}\)
=2020-1=2019