cho đa thức p(x) = (2x-1)6 +(x-2)7=a7x7+a6x6+...+a1x+a0. hãy tính giá trị của T=a7+a6+...+a1+a0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$a+b+c=0\Rightarrow a+b=-c$. khi đó:
$a^3+b^3+c^3=(a+b)^3-3ab(a+b)+c^3=(-c)^3-3ab(-c)+c^3$
$=-c^3+3abc+c^3=3abc$
Ta có đpcm.
ta có: a+b+c=0
=> c=-(a+b)
ta thay vào biểu thức:
=>a3+b3-(a+b)3=3ab(-a-b)
=>-3a2b-3ab2=-3a2b-3ab2

\(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)-105=0\)
\(\Leftrightarrow\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]-105=0\)
\(\Leftrightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)-105=0\) (1)
Đặt \(x^2+10x+20=t\), khi đó (1) trở thành:
\(\left(t-4\right)\left(t+4\right)-105=0\)
\(\Leftrightarrow t^2-16-105=0\)
\(\Leftrightarrow t^2-11^2=0\)
\(\Leftrightarrow\left(t-11\right)\left(t+11\right)=0\)
\(\Rightarrow\left(x^2+10x+20-11\right)\left(x^2+10x+20+11\right)=0\)
\(\Leftrightarrow\left(x^2+10x+9\right)\left(x^2+10x+31\right)=0\)
\(\Leftrightarrow\left(x^2+9x+x+9\right)\left[\left(x+5\right)^2+6\right]=0\)
\(\Leftrightarrow x\left(x+9\right)+\left(x+9\right)=0\) (vì \(\left(x+5\right)^2+6>0;\forall x\))
\(\Leftrightarrow\left(x+9\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+9=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-9\\x=-1\end{matrix}\right.\)
Vậy phương trình đã cho có tập nghiệm là $S=\{-9;-1\}$.
$Toru$
\(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)-105=0\\ \Leftrightarrow\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]=105\\ \Leftrightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)=105\\ \Leftrightarrow\left(x^2+10x+20-4\right)\left(x^2+10x+20+4\right)=105\\ \Leftrightarrow\left(x^2+10x+20\right)^2-4^2=105\\ \Leftrightarrow\left(x^2+10x+20\right)^2=121\\ \)
\(\Rightarrow\left[{}\begin{matrix}x^2+10x+20=11\left(1\right)\\x^2+10x+20=-11\left(2\right)\end{matrix}\right.\)
Giải (1):
\(x^2+10x+9=0\\ \Leftrightarrow\left(x^2+x\right)+\left(9x+9\right)=0\\ \Leftrightarrow x\left(x+1\right)+9\left(x+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x+9\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+1=0\\x+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-9\end{matrix}\right.\)
Giải (2):
Nhận thấy: \(x^2+10x+20=\left(x+5\right)^2-5\ge-5\forall x\inℝ\)
Vậy pt (2) vô nghiệm
Vậy tập nghiệm pt là: \(S=\left\{-1;-9\right\}\)

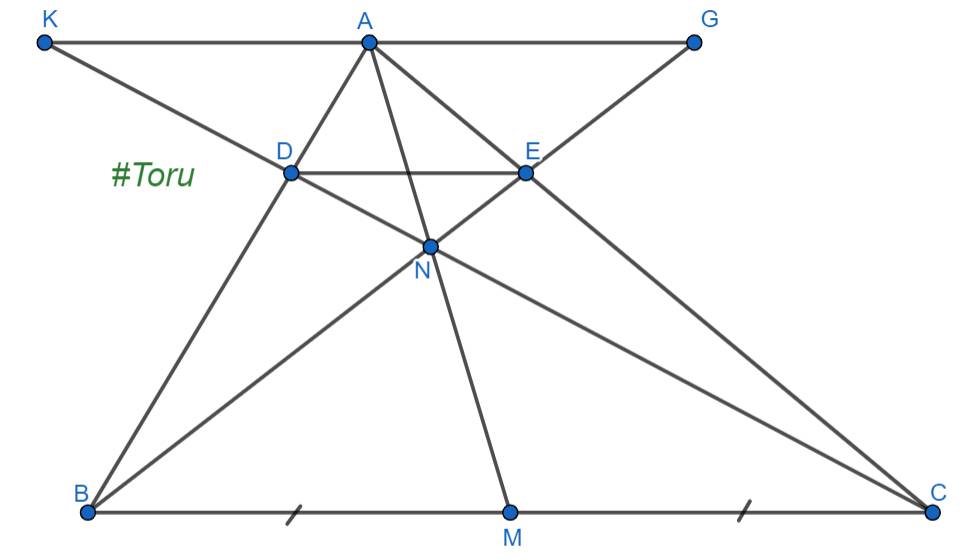
Kéo dài CD, BE sao cho chúng cắt đường thẳng song song với BC đi qua A lần lượt tại K, G.
Xét \(\Delta NMC\) có: \(AK//MC\text{ (}AK//BC;M\in BC)\)
\(\Rightarrow\dfrac{AN}{NM}=\dfrac{AK}{MC}\) (hệ quả đli Talet) (1)
Xét \(\Delta NMB\) có: \(AG//MB\text{ (}AG//BC;M\in BC)\)
\(\Rightarrow\dfrac{AN}{NM}=\dfrac{AG}{MB}\) (hệ quả đli Talet) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{AK}{MC}=\dfrac{AG}{MB}\)
Mà \(MB=MC\) (vì M là trung điểm BC) nên \(AK=AG\) (3)
Xét \(\Delta BDC\) có: \(AK//BC\Rightarrow \dfrac{AD}{BD}=\dfrac{AK}{BC}\) (hệ quả đli Talet) (4)
Xét \(\Delta CEB\) có: \(AG//BC\Rightarrow \dfrac{AE}{EC}=\dfrac{AG}{BC}\) (hệ quả đli Talet) (5)
Từ (3), (4) và (5) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{EC}\Rightarrow\dfrac{AD}{AD+BD}=\dfrac{AE}{AE+EC}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét \(\Delta ABC\) có: \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) (cmt) \(\Rightarrow DE//BC\) (đli Talet đảo)
\(\rightarrow\) Chọn C. Cả A và B đều đúng
$Toru$

Lời giải:
$A=a^3+b^3+c^3-3abc=(a^3+b^3)-3abc+c^3$
$=(a+b)^3-3ab(a+b)-3abc+c^3$
$=[(a+b)^3+c^3]-[3ab(a+b)+3abc]$
$=(a+b+c)[(a+b)^2-(a+b)c+c^2]-3ab(a+b+c)$
$=(a+b+c)[(a+b)^2-(a+b)c+c^2-2ab]$
$=(a+b+c)(a^2+b^2+c^2-ab-bc-ac)$

Bạn xem lại câu A nhé dãy A toàn các số hạng chia hết cho 3 mà số cuối 2023 lại không chia hết cho 3, dãy A không tuân theo quy luật nào cả không thể tính được bạn nhé
H = 2012.3+2012.4+...+2012.2011
= 2012.(3+4+...+2011)
Xét riêng: B=3+4+...+2011
Số số hạng dãy trên:
(2011-3):1+1=2009 (số hạng)
Tổng dãy B là:
(2011+3).2009:2=2023063
Do vậy: H = 2012.2023063 = 4070402756
Mình nghĩ bạn chép sai phần A của câu hỏi rồi vì mỗi số hạng đều chia hết cho 3 nên xin phép sửa nhé!
\(A=3+6+9+...+2022\)
Số số hạng của biểu thức A là:
\(\left(2022-3\right):3+1=674\) (số)
\(\Rightarrow A=\left(2022+3\right)\cdot674:2\)
\(\Rightarrow A=682425\)
Vậy \(\Rightarrow A=682425\)
\(H=2012\cdot3+2012\cdot4+...+2012\cdot2011\)
\(\Rightarrow H=2012\cdot\left(3+4+...+2011\right)\)
Đặt \(B=3+4+...+2011\)
Số số hạng của biểu thức B là:
\(\left(2011-3\right):1+1=2009\) (số)
\(\Rightarrow B=\left(2011+3\right)\cdot2009:2\)
\(\Rightarrow B=2023063\)
Thay \(B=2023063\) vào H được:
\(H=2012\cdot2023063\)
\(\Rightarrow H=4070402756\)
Vậy \(H=4070402756\)

\(A=3+6+9+...+2023\)
\(A=\left(2023-6\right)\div3+1=\dfrac{2020}{3}\rightarrow\) Đề sai.
\(B=2012.3+2012.4+...+2012.2011\)
\(B=2012.\left(3+4+...+2011\right)\)
Số số hạng:\(\left(2011-3\right)\div1+1=2009\) (số hạng)
Tổng : \(\left(2011+3\right).2009:2=2023063\)
Thay vào B , ta có:
\(B=2012.2023063=470402756\)

1: BC=BH+CH=4+9=13(cm)
Xét ΔHAB vuông tại H và ΔACB vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHAB~ΔACB
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC=4\cdot13=52\)
=>\(BA=\sqrt{52}=2\sqrt{13}\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=13^2-\left(2\sqrt{13}\right)^2=117\)
=>\(AC=\sqrt{117}=3\sqrt{13}\left(cm\right)\)
2: ΔHAB~ΔACB
=>\(\dfrac{HA}{AC}=\dfrac{AB}{CB}\)
=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{2\sqrt{13}\cdot3\sqrt{13}}{13}=6\left(cm\right)\)
Xét tứ giác AKHE có \(\widehat{AKH}=\widehat{AEH}=\widehat{KAE}=90^0\)
nên AKHE là hình chữ nhật
=>AH=KE
=>KE=6(cm)
3: Xét ΔAKH vuông tại K và ΔAHB vuông tại H có
\(\widehat{HAB}\) chung
Do đó: ΔAKH~ΔAHB
=>\(\dfrac{AK}{AH}=\dfrac{AH}{AB}\)
=>\(AH^2=AK\cdot AB\left(1\right)\)
Xét ΔAEH vuông tại E và ΔAHC vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔAHC
=>\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)
=>\(AH^2=AE\cdot AC\left(2\right)\)
Từ (1),(2) suy ra \(AK\cdot AB=AE\cdot AC\)
=>\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)
Xét ΔAKE vuông tại A và ΔACB vuông tại A có
\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)
Do đó: ΔAKE~ΔACB
4: ta có: ΔABC vuông tại A
mà AI là đường trung tuyến
nên IA=IC
=>ΔIAC cân tại I
=>\(\widehat{IAC}=\widehat{ICA}\)
ΔAKE~ΔACB
=>\(\widehat{AEK}=\widehat{ABC}\)
Ta có: \(\widehat{AEK}+\widehat{IAC}=\widehat{ABC}+\widehat{ACB}=90^0\)
=>EK\(\perp\)AI tại N
1. Tính AB, AC:
- Áp dụng định lý Pitago trong tam giác vuông AHB:
- AB² = AH² + HB²
- AH² = AB² - HB²
- Áp dụng định lý Pitago trong tam giác vuông AHC:
- AC² = AH² + HC²
- AH² = AC² - HC²
- Từ hai phương trình trên, ta có: AB² - HB² = AC² - HC²
- Suy ra: AB² = AC² - HC² + HB²
- Thay số: AB² = AC² - 9² + 4² = AC² - 65
- Áp dụng định lý Pitago trong tam giác vuông ABC:
- BC² = AB² + AC²
- BC² = (AC² - 65) + AC² = 2AC² - 65
- Thay BC = HB + HC = 4 + 9 = 13
- 13² = 2AC² - 65
- 2AC² = 13² + 65 = 224
- AC² = 112
- AC = √112 = 4√7 cm
- Thay AC vào phương trình AB² = AC² - 65:
- AB² = (4√7)² - 65 = 112 - 65 = 47
- AB = √47 cm
2. Tính KE:
- Áp dụng định lý Pitago trong tam giác vuông AKE:
- KE² = AK² + AE²
- Áp dụng định lý Pitago trong tam giác vuông AHB:
- AK² = AH² - HK²
- Áp dụng định lý Pitago trong tam giác vuông AHC:
- AE² = AH² - HE²
- Thay vào phương trình KE²:
- KE² = (AH² - HK²) + (AH² - HE²) = 2AH² - (HK² + HE²)
- Ta có: HK + HE = BC = 13 cm
- Áp dụng định lý Pitago trong tam giác vuông HKE:
- KE² = HK² + HE² = (HK + HE)² - 2HK.HE = 13² - 2HK.HE
- Suy ra: 2AH² - (HK² + HE²) = 13² - 2HK.HE
- 2AH² = 13² + 2HK.HE
- AH² = (13² + 2HK.HE) / 2
- Thay AH² = AB² - HB²:
- AB² - HB² = (13² + 2HK.HE) / 2
- 2(AB² - HB²) = 13² + 2HK.HE
- 2HK.HE = 2(AB² - HB²) - 13²
- HK.HE = (AB² - HB²) - 13²/2
- HK.HE = (47 - 4²) - 13²/2 = -65/2
- Vì HK và HE đều dương nên HK.HE = -65/2 là vô lý.
- Vậy, không thể tính KE bằng cách này.
3. Chứng minh AB.AK = AE.AC; AKE ~ ACB:
- Chứng minh AB.AK = AE.AC:
- Xét tam giác vuông AHB và tam giác vuông AHC, ta có:
- Góc BAH = Góc CAH (cùng bằng 90 độ)
- Góc ABH = Góc ACH (cùng phụ với góc BAH)
- Suy ra tam giác AHB đồng dạng với tam giác AHC (g-g)
- Do đó: AB/AC = AH/AH = 1
- Suy ra: AB = AC
- Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
- Góc KAE = Góc CAB (cùng bằng 90 độ)
- Góc AKE = Góc ACB (cùng phụ với góc KAE)
- Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)
- Do đó: AK/AC = AE/AB
- Suy ra: AB.AK = AE.AC
- Xét tam giác vuông AHB và tam giác vuông AHC, ta có:
- Chứng minh AKE ~ ACB:
- Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
- Góc KAE = Góc CAB (cùng bằng 90 độ)
- Góc AKE = Góc ACB (cùng phụ với góc KAE)
- Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)
- Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
4. Chứng minh AI vuông góc KE tại N:
- Xét tam giác ABC:
- I là trung điểm của BC nên AI là đường trung tuyến của tam giác ABC.
- Xét tam giác AKE:
- N là giao điểm của AI và KE nên N là trọng tâm của tam giác AKE.
- Theo tính chất trọng tâm của tam giác:
- Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
- Do đó: AN = 2/3 AI
- Xét tam giác vuông AHI:
- AI là đường trung tuyến của tam giác vuông AHI nên AI = 1/2 HI.
- Suy ra:
- AN = 2/3 AI = 2/3 * (1/2 HI) = 1/3 HI
- Do đó: IN = AI - AN = 1/2 HI - 1/3 HI = 1/6 HI
- Xét tam giác vuông HKE:
- N là trung điểm của KE nên HN là đường trung tuyến của tam giác vuông HKE.
- Theo tính chất đường trung tuyến của tam giác vuông:
- Đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
- Do đó: HN = 1/2 KE
- Suy ra:
- IN = 1/6 HI = 1/2 HN
- Do đó: HN = 3IN
- Xét tam giác HIN:
- HN = 3IN nên tam giác HIN vuông tại I (định lý đảo của định lý Pytago).
- Kết luận:
- AI vuông góc KE tại N.
Lưu ý:
- Trong bài toán này, không thể tính KE bằng cách sử dụng định lý Pitago trong tam giác vuông HKE vì HK.HE là một số âm.
- Việc chứng minh AB.AK = AE.AC và AKE ~ ACB là cần thiết để chứng minh AI vuông góc KE tại N.
- Việc chứng minh AI vuông góc KE tại N là một ứng dụng của tính chất trọng tâm của tam giác và tính chất đường trung tuyến của tam giác vuông.

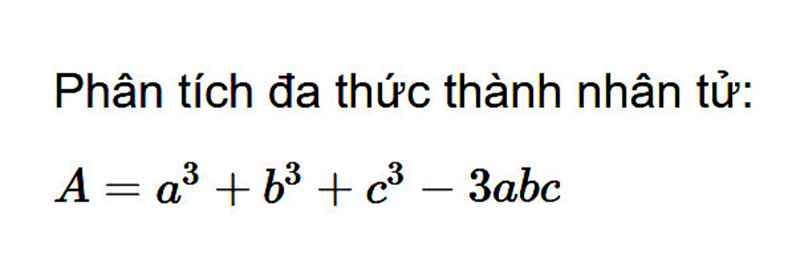
Lời giải:
Ta có:
$P(1)=(2.1-1)^6+(1-2)^7=a_7.1^7+a_6.1^6+....+a_1.1+a_0$
$\Rightarrow 1+(-1)=a_7+a_6+a_5+....+a_1+a_0$
$\Rightarrow a_7+a_6+a_5+....+a_1+a_0=0$