Hai ô tô đi từ A đến B vận tốc của xe thứ nhất là 60km/h xe thứ hai là 40km/h nên thời gian đi của xe thứ nhất ít hơn xe thứ hai là 30 phút. Tính quãng đường AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DA
2
10 tháng 1 2023
Vì `|x| >=0 forall x`.
`-> A = 11 + |4-x| >= 11 + 0 = 11`.
Dấu bằng xảy ra `<=> x = 4`.
DN
15 tháng 1 2023
Vì \(\left|4-x\right|\ge0\forall x\)
\(\Rightarrow11+\left|4-x\right|\ge11+0=11\)
\(\Rightarrow A\ge11\)
\(\Rightarrow\) GTNN của Alà 11\(\Leftrightarrow\left|4-x\right|=0\)
\(\left|4-x\right|=0\)
\(4-x=0\)
\(x=0+4=4\)
Vậy GTNN của A là 11 khi x = 4
NP
1
17 tháng 1 2023
Theo bài ra ta có :
x/5 = y/4 = z/7 và x+2y+z=10
=>x/5 = 2y/8 = z/7
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
x/5 = 2y/8 = z/7 = x+2y+z/5+8+7 = 10/20 =1/2
x= 5.1/2 x= 5/2
=> 2y=8.1/2 => y=2
z=7.1/2 z=7/2
Vậy .....
TT
0
10 tháng 1 2023
\(Câu\text{ }4:\\ Ta\text{ }có:\text{(x^2 – 3x + 2) + (4x^3– x^2+ x – 1)}\\ =x^2-3x+2+4x^3-x^2+x-1\\ =\text{4x}^3+\left(x^2-x^2\right)+\left(-3x+x\right)+\left(2-1\right)\\ =4x^3-2x+1\)
\(Câu\text{ }5:Đặt\text{ }tính\text{ }trừ\text{ }như\text{ }sau:\)
-x^3 -5x + 2 _ 3x + 8 x^3 -8x - 6
CT
Cô Tuyết Ngọc
Manager
VIP
10 tháng 1 2023
Em muốn hỏi bài nào vậy? Quá nhiều bài thầy cô và các bạn không thể trả lời được hết em ạ
S
11 tháng 1 2023
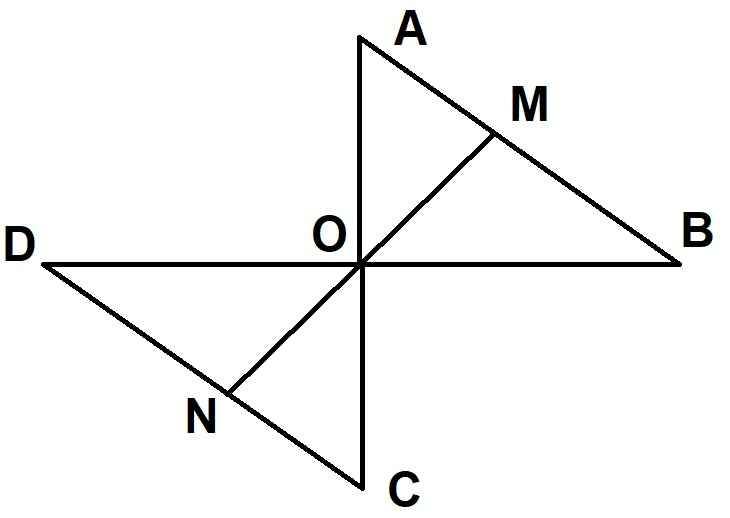
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)
S
10 tháng 1 2023
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)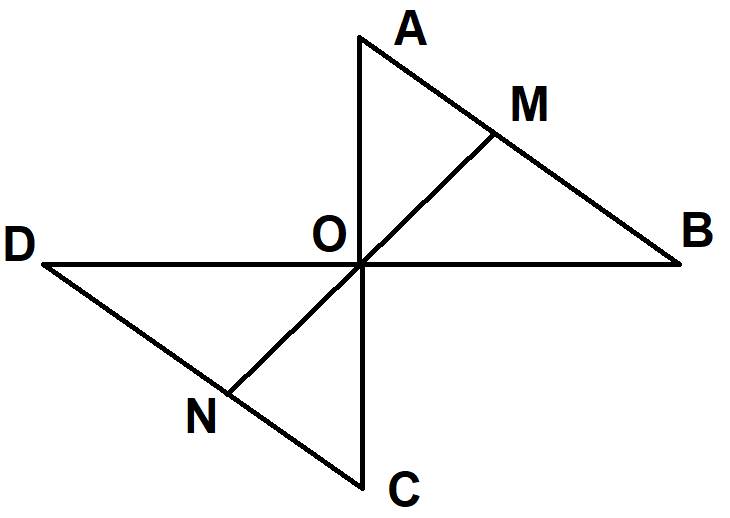
Đổi 30 phút = 0,5 giờ
Gọi thời gian xe thứ nhất, xe thứ hai đi hết quãng đường AB lần lượt là t1; t2 ( đk t1; t2 > 0)
Trên cùng một quãng đường vận tốc tỉ lệ nghịch với thời gian:
\(\dfrac{t_1}{t_2}\) = \(\dfrac{40}{60}\) = \(\dfrac{2}{3}\) ⇒ \(\dfrac{t_1}{2}\) = \(\dfrac{t_2}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{t_1}{2}\) = \(\dfrac{t_2-t_1}{3-2}\) = \(\dfrac{0,5}{1}\) = 0,5
t1 = 0,5 . 2 = 1 ( thỏa mãn)
Vậy thời gian xe thứ nhất đi hết quãng đường AB là 1 giờ
Quãng đường AB dài là: 60 x 1 = 60 (km)
Kết luận : Quãng đường AB dài 60 km
Gọi vận tốc của xe thứ hai là: a (km/h; a > 0)
vận tốc của xe thứ nhất là: 60%a = 35a35a
Gọi thời gian xe thứ nhất đi hết quãng đường AB là: b (h; b > 0)
thời gian xe thứ 2 đi hết quãng đường AB là: b - 3
Vì quãng đường đi như nhau nên thời gian và vận tốc là 2 đại lượng tỉ lệ nghịch ⇒a35a=bb−3=53⇒a35a=bb−3=53
⇒b5=b−33=b−(b−3)5−3=32⇒b5=b−33=b−(b−3)5−3=32 (theo tính chất của dãy tỉ số = nhau)
⇒b=32.5=152=7,5;b−3=7,5−3=4,5⇒b=32.5=152=7,5;b−3=7,5−3=4,5
Vậy thời gian xe thứ nhất đi hết quãng đường AB là 7,5 giờ, thời gian xe thứ 2 đi là 4,5 giờ
bạn iu dấu ơi nhớ tick nhé