Bài 6: Một hộp có 15 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số nguyên dương
không vượt quá 15, hai thẻ khác nhau thì ghi hai số khác nhau. Lấy ngẫu nhiên một chiếc thẻ
từ trong hộp, ghi lại số của thẻ lấy ra và bỏ lại thẻ đó vào hộp. Sau 30 lần lấy thẻ liên tiếp,
thẻ ghi số 7 được lấy ra 6 lần.
a. Tính xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số 7” trong trò chơi trên.
b. Nêu mối liên hệ giữa xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số là số nguyên tố”
với xác suất của biến cố đó khi số lần rút thẻ ngày càng lớn
giúp tui với !!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 891+(359+109)
=891+109+359
=1000+359=1359
b: \(\dfrac{19}{11}+\left(\dfrac{5}{13}+\dfrac{3}{11}\right)\)
\(=\dfrac{19}{11}+\dfrac{3}{11}+\dfrac{5}{13}\)
\(=2+\dfrac{5}{13}=\dfrac{31}{13}\)
c: \(\dfrac{17,8\cdot3,7-7,8\cdot4,8+5,7\cdot17,8-4,6\cdot7,8}{11,2+12,3+13,4-12,6-11,5-10,4}\)
\(=\dfrac{17,8\left(3,7+5,7\right)-7,8\left(4,8+4,6\right)}{11,2-10,4+12,3-11,5+13,4-12,6}\)
\(=\dfrac{17,8\cdot9,4-7,8\cdot9,4}{0,8+0,8+0,8}=\dfrac{9,4\cdot10}{2,4}=\dfrac{94}{2,4}=\dfrac{940}{24}=\dfrac{235}{6}\)
\(a,891+\left(359+109\right)\\ =\left(891+109\right)+359\\ =1000+359\\ =1359\\ b,\dfrac{19}{11}+\left(\dfrac{5}{13}+\dfrac{3}{11}\right)\\ =\left(\dfrac{19}{11}+\dfrac{3}{11}\right)+\dfrac{5}{13}\\ =2+\dfrac{5}{13}\\ =\dfrac{26}{13}+\dfrac{5}{13}\\ =\dfrac{31}{13}\\ c,\dfrac{17,8\times3,7-7,8\times4,8+5,7\cdot17,8-4,6\times7,8}{11,2+12,3+13,4-12,6-11,5-10,4}\\ =\dfrac{17,8\times\left(3,7+5,7\right)-7,8\times\left(4,8+4,6\right)}{\left(11,2+12,3-11,5\right)+\left(13,4-10,4\right)-12,6}\\ =\dfrac{17,8\times9,4-7,8\times9,4}{12+3-12,6}\\ =\dfrac{9,4\times\left(17,8-7,8\right)}{2,4}\\ =\dfrac{94}{2,4}\\ =\dfrac{940}{24}=\dfrac{235}{6}\)

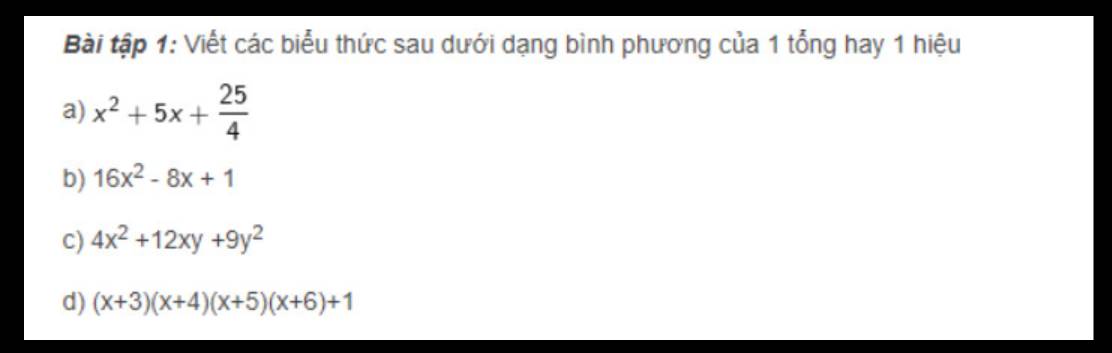
a: \(x^2+5x+\dfrac{25}{4}=x^2+2\cdot x\cdot\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2=\left(x+\dfrac{5}{2}\right)^2\)
b: \(16x^2-8x+1=\left(4x\right)^2-2\cdot4x\cdot1+1^2=\left(4x-1\right)^2\)
c: \(4x^2+12xy+9y^2=\left(2x\right)^2+2\cdot2x\cdot3y+\left(3y\right)^2=\left(2x+3y\right)^2\)
d: \(\left(x+3\right)\left(x+4\right)\left(x+5\right)\left(x+6\right)+1\)
\(=\left(x^2+9x+18\right)\left(x^2+9x+20\right)+1\)
\(=\left(x^2+9x\right)^2+38\left(x^2+9x\right)+360+1\)
\(=\left(x^2+9x\right)^2+2\cdot\left(x^2+9x\right)\cdot19+19^2\)
\(=\left(x^2+9x+19\right)^2\)

\(\dfrac{890}{100}=\dfrac{89}{10}=8,9\)
\(\dfrac{900}{1000}=\dfrac{9}{10}=0,9\)

B là tập hợp của các số lẻ từ 7 đến 86
=>B={7;9;11;13;15;17;19;21;23;...;85}
Số thứ 10 từ trái qua là 25
Giải
Các số tự nhiên lẻ từ 7 đến 86 là các số tự nhiên thuộc dãy số sau:
7; 9; 11; 13; 15;...; 85
Dãy số trên là dãy số cách đều với khoảng cách là:
9 - 7 = 2
Số thứ 10 của dãy số trên là: 2 x (10 - 1) + 7 = 25
Từ những lập luận trên ta có kết luận:
B = {7; 9; 11; 13; 15;...; 85}
Tính từ trái qua phải phần tử thứ 10 của tập B là 25.

\(x+0,25=\dfrac{43}{4}-\dfrac{18}{5}\\ x+0,25=7,15\\ x=7,15-0,25\\x=6,9\)
Vậy x = 6,9

\(A=\left(-7\right)+\left(x+1\right)^2\)
Nhận xét: \(\left(x+1\right)^2\ge0\)
\(\Rightarrow\left(-7\right)+\left(x+1\right)^2\ge-7\)
hay \(A\ge-7\)
Dấu "=" xảy ra khi:
\(x+1=0\)
\(\Rightarrow x=-1\)
Vậy...
\(B=\left(x-2\right)^2-17\)
Nhận xét: \(\left(x-2\right)^2\ge0\)
\(\Rightarrow\left(x-2\right)^2-17\ge-17\)
hay \(A\ge-17\)
Dấu "=" xảy ra khi:
\(x-2=0\)
\(\Rightarrow x=2\)
Vậy...
a: Xác suất thực nghiệm của biến cố "Thẻ lấy ra ghi số 7" là:
\(\dfrac{6}{30}=\dfrac{1}{5}\)
b: Gọi A là biến cố "Thẻ rút ra là số nguyên tố"
=>A={2;3;5;7;11;13}
=>n(A)=6
=>\(P_A=\dfrac{6}{15}=\dfrac{2}{5}\)
=>Khi số lần rút thẻ ngày càng lớn thì xác suất thực nghiệm của biến cố A ngày càng gần với 2/5