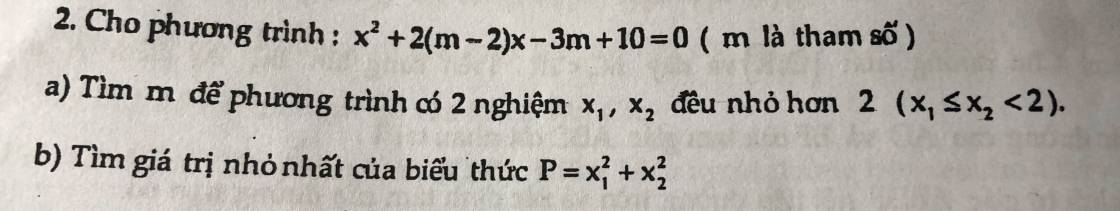
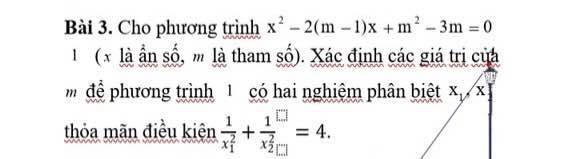
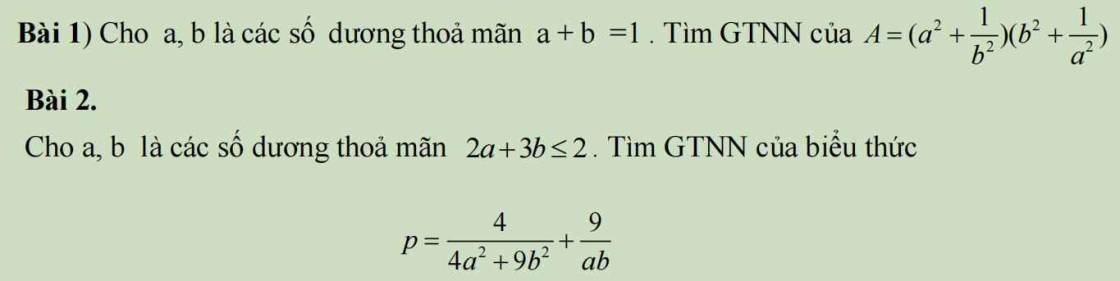
a: Xét tứ giác MDBO có \(\widehat{DMO}+\widehat{DBO}=90^0+90^0=180^0\)

nên MDBO là tứ giác nội tiếp

b: Xét (O) có

CA,CM là các tiếp tuyến

Do đó: CA=CM và OC là phân giác của góc MOA

Xét (O) có

DM,DB là các tiếp tuyến

Do đó: DM=DB và OD là phân giác của góc MOB

Ta có: \(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)

=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)

=>\(2\cdot\widehat{COD}=180^0\)

=>\(\widehat{COD}=90^0\)

Xét ΔOCD vuông tại O có OM là đường cao

nên \(OM^2=MC\cdot MD\)

=>\(OM^2=AC\cdot BD\)

c: Xét (O) có

ΔMAB nội tiếp

AB là đường kính

Do đó: ΔMAB vuông tại M

Xét ΔMAB vuông tại M có \(sinBAM=\dfrac{BM}{BA}\)

=>\(\dfrac{BM}{2R}=sin60=\dfrac{\sqrt{3}}{2}\)

=>\(BM=R\sqrt{3}\)

=>\(AM=\sqrt{\left(2R\right)^2-\left(R\sqrt{3}\right)^2}=R\)

ΔMAB vuông tại M

=>\(S_{MAB}=\dfrac{1}{2}\cdot MA\cdot MB=\dfrac{1}{2}\cdot R\cdot R\sqrt{3}=\dfrac{R^2\sqrt{3}}{2}\)

a) \(\Delta'=\left(m-2\right)^2-\left(-3m+10\right)=m^2-m-6\)

Để phương trình có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-2\\m\ge3\end{matrix}\right.\) (1)

Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=4-2m\\x_1x_2=-3m+10\end{matrix}\right.\)

Để phương trình có 2 nghiệm x₁, x₂ đều nhỏ hơn 2 \(\left(x_1\le x_2< 2\right)\) thì:

\(\left\{{}\begin{matrix}\left(x_1-2\right)+\left(x_2-2\right)< 0\\\left(x_1-2\right)\left(x_2-2\right)>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2< 4\\x_1x_2-2\left(x_1+x_2\right)+4>0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}4-2m< 4\\-3m+10-2\left(4-2m\right)+4>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-2m< 0\\m+6>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\m>-6\end{matrix}\right.\Leftrightarrow m>0\)

Kết hợp với điều kiện (1), ta được: \(m\ge3\)

\(Toru\)

x² -(2m+1)x+2m=0 (a=1; b = -(2m+1); c= 2m)
Δ= b²- 4ac= [-(2m+1)]²-4.1.2m= 4m² +4m+1-8m =4m²-4m+1

= (2m-1)²

Phương trình có hai nghiệm phân biệt khi (2m-1)²>0

<=> 2m-1 >0 <=> m > 1/2

Vậy: với m>1/2 thì phương trình có hai nghiệm phân biệt
Vì với m>1/2 thì phương trình có hai nghiệm nên theo hệ thức Vi-ét, ta có:
x₁+x₂= -b/a= 2m+1
x₁.x₂= c/a = 2m
Ta có: