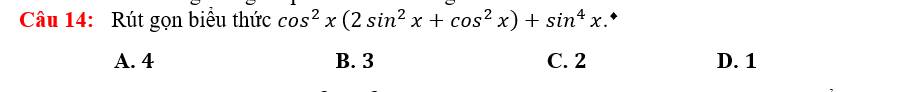giải phương tình sau:
\(\dfrac{1}{\sin x}\)+\(\dfrac{1}{\sin\left(x-\dfrac{3\pi}{2}\right)}\)= 4\(\sin\left(\dfrac{7\pi}{4}-x\right)\)Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\cos^4x+2\cos^2x\sin^2x+\sin^4x=\)
\(=\left(\cos^2x+\sin^2x\right)^2=1\)
\(cos^2x\left(2sin^2x+cos^2x\right)+sin^4x=cos^4x+2sin^2x.cos^2x+sin^4x\)
\(=\left(cos^2x+sin^2x\right)^2=1\)

\(\Leftrightarrow\left(4x^2-3x+1\right)^2< \left(x+1\right)^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x^2-3x+1>-\left(x+1\right)\\4x^2-3x+1< x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x^2-2x+2>0\\4x^2-4x< 0\end{matrix}\right.\)
\(\Rightarrow0< x< 1\)

\(\left(C\right):\left(x-1\right)^2+\left(y-2\right)^2=10\) tâm \(I\left(1,2\right)\) bán kính \(R=\sqrt{10}\)
Vì tam giác \(ABC\) đều nên \(AI\) vuông góc với \(BC\), \(I\) là trọng tâm tam giác \(ABC\) nên \(AI=2d\left(I,BC\right)\Rightarrow d\left(I,BC\right)=\dfrac{AI}{2}=\dfrac{R}{2}=\dfrac{\sqrt{10}}{2}\).
Ta có: \(AI\) đi qua \(A\left(0,-1\right)\) và \(I\left(1,2\right)\) suy ra phương trình đường thẳng \(AI\) là \(3x-y-1=0\) suy ra \(BC\): \(x+3y+c=0\)
\(d\left(I,BC\right)=\dfrac{\left|1+3.2+c\right|}{\sqrt{1^2+3^2}}=\dfrac{\left|c+7\right|}{\sqrt{10}}=\dfrac{\sqrt{10}}{2}\Leftrightarrow\left[{}\begin{matrix}c=-2\\c=-12\end{matrix}\right.\)
Với \(c=-12\): \(BC:x+3y-12=0\)
\(\left(0-3-12\right)\left(1+2.3-12\right)>0\) nên \(A,I\) nằm cùng phía so với \(BC\) (loại).
Vậy \(c=-2\): \(BC:x+3y-2=0\)
Tọa độ hai điểm \(B,C\) chính là giao điểm của đường thẳng \(BC\) và đường tròn \(\left(C\right)\).
\(x+3y-2=0\Leftrightarrow x=2-3y\)
\(\left(2-3y-1\right)^2+\left(y-2\right)^2=10\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{1+\sqrt{3}}{2}\Rightarrow x=\dfrac{1-3\sqrt{3}}{2}\\y=\dfrac{1-\sqrt{3}}{2}\Rightarrow x=\dfrac{1+3\sqrt{3}}{2}\end{matrix}\right.\)
Ta có tọa độ hai điểm \(B,C\).

Đường tròn (C) có tâm \(I\left(\dfrac{3}{2};-2\right)\Rightarrow\overrightarrow{IM}=\left(-\dfrac{5}{2};5\right)=-\dfrac{5}{2}\left(1;-2\right)\)
Đường thẳng d tiếp xúc (C) tại M nên \(IM\perp d\Rightarrow d\) nhận (1;-2) là 1 vtpt
Phương trình tiếp tuyến d:
\(1\left(x+1\right)-2\left(y-3\right)=0\Leftrightarrow x-2y+7=0\)

lấy bán kính chia cho độ dài cung sẽ ra được số đo radian


Gọi tâm đường tròn là \(I\left(a;b\right)\Rightarrow IA=IB=d\left(I;Ox\right)=b\)
\(\left\{{}\begin{matrix}\overrightarrow{AI}=\left(a-1;b-1\right)\\\overrightarrow{BI}=\left(a-1;b-4\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AI^2=\left(a-1\right)^2+\left(b-1\right)^2\\BI^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
\(AI^2=BI^2\Rightarrow\left(b-1\right)^2=\left(b-4\right)^2\)
\(\Rightarrow-2b+1=-8b+16\Rightarrow b=\dfrac{5}{2}\)
Lại có:
\(IA=b\Rightarrow IA^2=b^2\Rightarrow\left(a-1\right)^2+\left(\dfrac{5}{2}-1\right)^2=\left(\dfrac{5}{2}\right)^2\)
\(\Rightarrow\left(a-1\right)^2=4\Rightarrow\left[{}\begin{matrix}a=3\\a=-1\end{matrix}\right.\)
Có 2 đường tròn thỏa mãn: \(\left[{}\begin{matrix}\left(x-3\right)^2+\left(y-\dfrac{5}{2}\right)^2=\dfrac{25}{4}\\\left(x+1\right)^2+\left(y-\dfrac{5}{2}\right)^2=\dfrac{25}{4}\end{matrix}\right.\)

có làm thì mới có ăn ko làm mà đòi có ăn thì ăn đồng bằng ăn cát
có làm thì mới có ăn ko làm mà đòi có ăn thì ăn đồng bằng ăn cát