chứng minh 1/1+2+3+4+...+n = 2.(1/n-1/n+1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


cho diện tích hình thang là 124,7 m vuông đáy lón là 15, đái bé là 14m, tính chiều cao

\(\dfrac{x}{y}=\dfrac{1}{3}\) thì \(\dfrac{y}{x}=\dfrac{3}{1}=3\) hay \(y=3x\).
Ta có:
\(N=\dfrac{x-y}{x+3y}\)
\(\Rightarrow N=\dfrac{x-3x}{x+3\left(3x\right)}\)
\(\Rightarrow N=\dfrac{-2x}{x+9x}\)
\(\Rightarrow N=\dfrac{-2x}{10x}=\dfrac{-2}{10}=-5\)

\(\dfrac{x}{-5}=\dfrac{y}{9}=\dfrac{z}{11}\) và \(x-z=-32\)
Ta có\(\dfrac{x}{-5}=\dfrac{z}{11}=\dfrac{x-z}{-5-11}=-\dfrac{32}{-16}=2\)
\(\left\{{}\begin{matrix}x=2\cdot\left(-5\right)=-10\\y=2\cdot9=18\\z=2\cdot11=22\end{matrix}\right.\)
Vậy x=-10
y=18
z=22


\(\dfrac{14}{21}=\dfrac{42}{x}\)
\(14x=42.21\)
\(14x=882\)
x = 63

Để chứng minh điều trên ta xét dãy số:
\(A=1-3+3^2-3^3+...+3^{98}-3^{99}\)
\(3A=3-3^2+3^3-3^4+...+3^{99}-3^{100}\)
\(3A+A=\left(3-3^2+3^3-...-3^{100}\right)+\left(1-3+...+3^{98}-3^{99}\right)\)
\(4A=1-3^{100}\)
\(A=\dfrac{1-3^{100}}{4}\)
=> \(1-3^{100}⋮4\)
hay \(3^{100}:4\) ( dư 1) (đcpcm)

Điểm số của An bằng \(\dfrac{5}{6}\) điểm số của Bình, điểm số của yên bằng 50% số điểm của An hay điểm số mỗi bạn Yên, An, Bình có tỉ lệ lần lượt là \(\left(5\cdot50\%\right):5:6=2,5:5:6\).
Gọi số tiền mỗi bạn nhận được lần lượt là \(x,y,z\), ta có:
\(\dfrac{x}{2,5}=\dfrac{y}{5}=\dfrac{z}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2,5}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y+z}{2,5+5+6}=\dfrac{480000}{13,5}=\dfrac{320000}{9}\)
Suy ra:
\(x=2,5\cdot\dfrac{320000}{9}\approx88889\left(đồng\right)\)
\(y=5\cdot\dfrac{320000}{9}\approx177778\left(đồng\right)\)
\(z=6\cdot\dfrac{320000}{9}\approx213333\left(đồng\right)\)
Vậy Yên có 88 889 đồng, An có 177 778 đồng, Bình có 213 333 đồng

\(1+\dfrac{1}{2}\left(1+2\right)+\dfrac{1}{3}\left(1+2+3\right)+...+\dfrac{1}{20}\left(1+2+...+20\right)\)
\(=1+\dfrac{3\cdot2\div2}{2}+\dfrac{4\cdot3\div2}{3}+...+\dfrac{21\cdot20\div2}{20}\)
\(=1+\dfrac{3}{2}+2+...+\dfrac{21}{2}\) (A)
Trong (A) có \(\dfrac{\dfrac{21}{2}-1}{\dfrac{3}{2}-1}+1=20\) (số hạng)
Suy ra \(\left(A\right)=\left(\dfrac{21}{2}+1\right)\cdot20\div2=115\)
Vậy \(1+\dfrac{1}{2}\left(1+2\right)+\dfrac{1}{3}\left(1+2+3\right)+...+\dfrac{1}{20}\left(1+2+...+20\right)=115\)

Lời giải:
$A=1-3+3^2-3^3+3^4-....+3^{38}-3^{39}$
$3A=3-3^2+3^3-3^4+3^5-...+3^{39}-3^{40}$
$A+3A=(1-3+3^2-3^3+3^4-....+3^{38}-3^{39})+(3-3^2+3^3-3^4+3^5-...+3^{39}-3^{40})$
$4A=1-3^{40}$
b.
Xét $B=1-3+3^2-3^3+....+3^{98}-3^{99}$
$3B=3-3^2+3^3-3^4+....+3^{99}-3^{100}$
$\Rightarrow B+3B=1-3^{100}$
$4B=1-3^{100}$
$3^{100}=1-4B$
Suy ra $3^{100}$ chia $4$ dư $1$
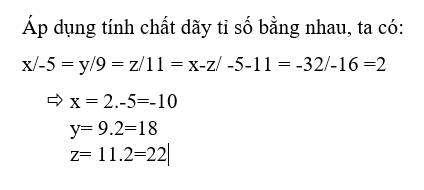
Lời giải:
$\frac{1}{1+2+3+...+n}=\frac{1}{\frac{n(n+1)}{2}}=\frac{2}{n(n+1)}$
$=2.\frac{(n+1)-n}{n(n+1)}=2[\frac{n+1}{n(n+1)}-\frac{n}{n(n+1)}]$
$=2(\frac{1}{n}-\frac{1}{n+1})$ (đpcm)