Ta có \(A=\frac{3}{4}x+\frac{1}{x}+\frac{2}{y^2}+y=\left(\frac{x}{4}+\frac{1}{x}\right)+\left(\frac{2}{y^2}+\frac{y}{4}+\frac{y}{4}\right)+\left(\frac{x}{2}+\frac{y}{2}\right)\)

Lại có \(\frac{x}{4}+\frac{1}{x}\ge2\sqrt{\frac{x}{4}.\frac{1}{x}}=1\);\(\frac{2}{y^2}+\frac{y}{4}+\frac{y}{4}\ge3\sqrt[3]{\frac{2}{y^2}.\frac{y}{4}.\frac{y}{4}}=\frac{3}{2}\)

             \(\frac{x+y}{2}\ge\frac{4}{2}=2\)

=>\(A\ge1+\frac{3}{2}+2=\frac{9}{2}\)

=>\(MinA=\frac{9}{2}\) xảy ra khi x=y=2

sau đừng phát ngôn vậy nha em =)))

b, sửa  \(\frac{6}{\sqrt{13}-1}+\frac{6}{\sqrt{13}+1}\)

\(=\frac{6\sqrt{13}+6+6\sqrt{13}-6}{12}=\frac{12\sqrt{13}}{12}=\sqrt{13}\)

b, sai rồi em

a, \(\frac{2}{3+\sqrt{2}}+\frac{1}{3-\sqrt{2}}=\frac{6-2\sqrt{2}+3+\sqrt{2}}{7}=\frac{9-\sqrt{2}}{7}\)

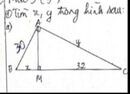
Xét tam giác ABC vuông tại A, đường cao AH

* Áp dụng hệ thức :

 \(AB^2=BM.BC\Rightarrow900=BM\left(32+BM\right)\)

\(\Leftrightarrow BM^2+32BM-900=0\Leftrightarrow BM=x=18\)cm 

=> BC = x + y = 18 + 32 = 50 cm 

* Áp dugnj hệ thức : \(AC^2=MC.BC=32.50\Rightarrow AC=y=\sqrt{32.50}=40\)cm 

a) Số số hạng : ( 100 - 1 ) : 1 + 1 = 100 

    Tổng : ( 100 + 1 ) x 100 : 2 = 5050

b) Số số hạng : ( 100 - 2 ) : 2 + 1 = 50 

    Tổng : ( 100 + 2 ) x 50 : 2 = 2550

c) Số số hạng : ( 99 - 1 ) : 2 + 1 = 50

    Tổng : ( 99 + 1 ) x 50 : 2 = 2500

a)A=1+2+3+4+...+100

 Số số hạng là: ( 100 - 1 ) : 1 + 1 =100

 Tổng các số hạng là: ( 100 + 1 ) x 100 : 2 = 5050

 Vậy A = 5050

b)B=2+4+6+...+100

 Số số hạng là: ( 100 - 2 ) : 2 + 1 = 50

 Tổng các số hạng là: ( 100 + 2 ) x 50 : 2 = 2550

  Vậy B = 2550

Cau c tớ chưa bt , ,mong bn k ạ

Với x > = 0 

a, Ta có : \(\sqrt{x}+3\ge3\Rightarrow P=\frac{3}{\sqrt{x}+3}\le\frac{3}{3}=1\)

Dấu ''='' xảy ra khi x = 0 

Vậy GTLN của P bằng 1 tại x = 0