cho tam giác abc nhọn có AB<AC . Tia phân giác góc A cắt BC tại D . Chứng minh rằng DB<DC ( bài này là quan hệ giữa góc và cạnh đối diện trong 1 tam giác nha)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi vận tốc xe 1 là x
=> vận tốc xe 2 là 1,25x
=> Trong 2 giờ xe 1 đi được 2.x
Trong 2 giờ xe 2 đi được 2.(1,25x).
Mà khoảng cách 2 xe là 20km => ta tính được x.
Từ đó có vận tốc, nhân số giờ để ra quãng đường mỗi xe đã đi.
Chúc em học tốt!

Để chắc chắn lấy ra số bi đỏ, trong trường hợp xấu nhất bốc hết bi màu khác nhưng chưa có viên đỏ nào, ta lấy thêm 5 viên nữa chắc chắn là viên đỏ.
Bài này em cung cấp thông tin không đúng hoặc sai, nên anh chỉ hướng dẫn được hướng làm là như v thôi nhé.
Chúc em học tốt!

a) NM nhỏ hơn NE
b) góc PEN = góc EMN + góc ENM (theo định lý góc ngoài của tam giác)
Mà góc EMN vuông tại M, tức là 90 độ
=> góc PEN luôn lớn hơn 90 độ
=> Điều phải chứng minh.
Chúc em học tốt!

(Hình minh họa)
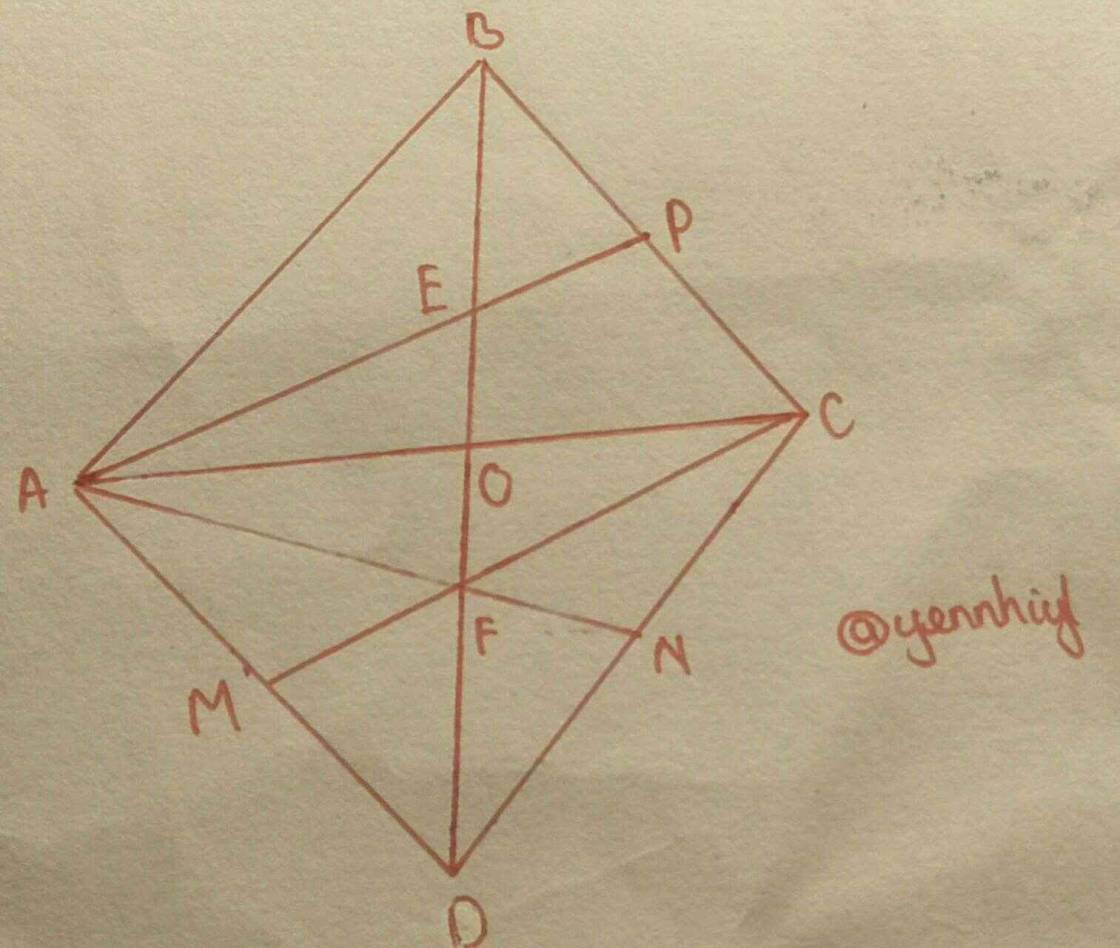
a)
Gọi O là giao điểm của AC và BD
Xét \(\Delta ABD\) và \(\Delta CDB\):
BD chung
\(\widehat{ABD}=\widehat{CDB}\)
\(\widehat{ADB}=\widehat{CBD}\)
\(\Rightarrow\Delta ABD=\Delta CBD\left(g.c.g\right)\)
\(\Rightarrow AB=CD\)
Xét \(\Delta AOB\) và \(\Delta COD\):
AB = CD
\(\widehat{OBA}=\widehat{ODC}\)
\(\widehat{OAB}=\widehat{OCD}\)
\(\Rightarrow\Delta AOB=\Delta COD\left(g.c.g\right)\)
\(\Rightarrow OA=OC;OB=OD\)
\(\Rightarrow O\) là trung điểm AC và BD
Xét \(\Delta ACD\):
MC và DO là hai đường trung tuyến của tam giác và giao nhau ở F
\(\Rightarrow F\) là trọng tâm \(\Delta ADC\)
Mà AN là đường trung tuyến \(\Delta ADC\)
\(\Rightarrow A,F,N\) thẳng hàng
b)
Vì P là trọng tâm \(\Delta ADC\)
\(\Rightarrow DF=\dfrac{2}{3}DO;OF=\dfrac{1}{3}DO\)
Vì O là giao điểm của hai đường trung tuyến BO và AP của \(\Delta ABC\)
\(\Rightarrow O\) là trọng tâm \(\Delta ABC\)
\(\Rightarrow BE=\dfrac{2}{3}BO;EO=\dfrac{1}{3}BO\)
Mà O là trung điểm BD
\(\Rightarrow BO=DO\)
\(\Rightarrow BE=DF=\dfrac{2}{3}BO=\dfrac{2}{3}DO\)
\(\Rightarrow FO=EO=\dfrac{1}{3}BO=\dfrac{1}{3}DO\Rightarrow EO+FO=FE=\dfrac{2}{3}BO=\dfrac{2}{3}DO\)
\(\Rightarrow BE=FE=FD\).

a. Tính góc ADB và góc BDC: Gọi góc ADB = x, góc BDC = y. Ta có thể sử dụng các quy tắc góc chắn cung và góc nội tiếp để tính góc như sau:
- Góc BAC = 90 độ (do tam giác ABC vuông tại A)
- Góc B = 60 độ (theo đề bài)
- Góc ABC = 180 - Góc BAC - Góc B = 30 độ (tổng các góc của tam giác ABC bằng 180 độ)
- Góc ABD = Góc ABC (do AB // CD theo định lý Thales)
- Góc DAB = 180 - Góc ADB - Góc ABD = 180 - x - 30
- Góc BCD = Góc BAC (do CD là tiếp tuyến của đường tròn ngoại tiếp tam giác BDC)
- Góc BDC = 180 - Góc BCD - Góc B = 90 - Góc BAC/2 = 45 độ (do tam giác BCD cân tại B)
b. So sánh các cạnh của tam giác ABD: Để so sánh các cạnh của tam giác ABD, ta cần tính độ dài các cạnh. Theo định lý Pythagoras trong tam giác vuông ABC, ta có:
- AB^2 = AC^2 + BC^2 = a^2 + b^2
- BC = a
- AC = b Vậy AB = sqrt(a^2 + b^2). Tương tự, ta có CD = b và BD = c*sqrt(3)/2 (tính theo phương pháp trong câu trả lời trước). Do đó, ta có thể so sánh các cạnh của tam giác ABD theo thứ tự tăng dần: CD < AB < BD.
c. So sánh các góc của tam giác BDC: Trong tam giác BDC, ta đã tính được góc BDC = 45 độ (như ở câu a). Do tam giác BDC cân tại B, nên góc CBD cũng bằng 45 độ. Vì vậy, hai góc của tam giác BDC bằng nhau và bằng 45 độ.
a. Tính góc ADB và góc BDC: Gọi góc ADB = x, góc BDC = y. Ta có thể sử dụng các quy tắc góc chắn cung và góc nội tiếp để tính góc như sau:
- Góc BAC = 90 độ (do tam giác ABC vuông tại A)
- Góc B = 60 độ (theo đề bài)
- Góc ABC = 180 - Góc BAC - Góc B = 30 độ (tổng các góc của tam giác ABC bằng 180 độ)
- Góc ABD = Góc ABC (do AB // CD theo định lý Thales)
- Góc DAB = 180 - Góc ADB - Góc ABD = 180 - x - 30
- Góc BCD = Góc BAC (do CD là tiếp tuyến của đường tròn ngoại tiếp tam giác BDC)
- Góc BDC = 180 - Góc BCD - Góc B = 90 - Góc BAC/2 = 45 độ (do tam giác BCD cân tại B)
b. So sánh các cạnh của tam giác ABD: Để so sánh các cạnh của tam giác ABD, ta cần tính độ dài các cạnh. Theo định lý Pythagoras trong tam giác vuông ABC, ta có:
- AB^2 = AC^2 + BC^2 = a^2 + b^2
- BC = a
- AC = b Vậy AB = sqrt(a^2 + b^2). Tương tự, ta có CD = b và BD = c*sqrt(3)/2 (tính theo phương pháp trong câu trả lời trước). Do đó, ta có thể so sánh các cạnh của tam giác ABD theo thứ tự tăng dần: CD < AB < BD.
c. So sánh các góc của tam giác BDC: Trong tam giác BDC, ta đã tính được góc BDC = 45 độ (như ở câu a). Do tam giác BDC cân tại B, nên góc CBD cũng bằng 45 độ. Vì vậy, hai góc của tam giác BDC bằng nhau và bằng 45 độ.