Tính giá trị biểu thức:
S=1/1.2+1/2.3+1/3.4+...+1/2017.2018
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Tam giác ABC cân tại A nên \(\widehat{B}\) = \(\widehat{C}\)
⇒ \(\widehat{ABM}\) = \(\widehat{ACN}\) (1)
AB = AC (2)
\(\widehat{BAM}\) = \(\widehat{CAN}\) = 900 (3)
Kết hợp (1); (2) ; (3) ta có △BAM = △CAN (g-c-g)
b, BM = CN ( Δ BAM = ΔCAN)
BM = BN + MN = MN + MC
⇒ BN = CM
c, \(\widehat{BAN}\) + \(\widehat{NAC}\) = \(\widehat{BAC}\) =1200
\(\Rightarrow\) \(\widehat{BAN}\) = 1200 - \(\widehat{NAC}\) = 1200 - 900 = 300
\(\widehat{ABN}\) = (1800 - 1200) : 2 = 300
⇒ \(\widehat{BAN}\) = \(\widehat{ABN}\) = 300 ⇒ △ANB cân tại N

a) Xét hai tam giác BADBAD và BFDBFD có:
ABD^=FBD^ABD
=FBD
(vì BDBD là tia phan giác của góc BB);
AB=BFAB=BF (ΔABFΔABF cân tại BB);
BDBD là cạnh chung;
Vậy ΔBAD=ΔBFDΔBAD=ΔBFD (c.g.c).
b) ΔBAD =Δ BFDΔBAD =Δ BFD suy ra BAD^=BFD^=100∘BAD
=BFD
=100∘ (hai góc tương ứng).
Suy ra DFE^=180∘−BFD^=80∘DFE
=180∘−BFD
=80∘. (1)
Tam giác ABCABC cân tại AA nên B^=C^=180∘−100∘2=40∘B
=C
=2180∘−100∘=40∘
Suy ra DBE^=20∘DBE
=20∘.
Tương tự, tam giác BDEBDE cân tại BB nên BED^=180∘−20∘2=80∘BED
=2180∘−20∘=80∘. (2)
Từ (1) và (2) suy ra ΔDEFΔDEF cân tại DD.

x3 - 3x2 + x + 1
- 2x3 - x2 + 3x - 4
_________________
-x3 - 2x2 - 2x + 5
P(x) - Q(x) = -x3 - 2x2 - 2x + 5
b, Thay x = 1 vào P(x); Q(x) ta có :
P(1) = 13 - 3.12 + 1 + 1 = 0
Q(1) = 2.13 - 12 + 3.1 - 4 = 0
Vậy 1 là nghiệm của cả hai đa thức P(x) và Q(x)
a) Ta có P(x)−Q(x)=(x3−3x2+x+1)−(2x3−x2+3x−4)P(x)−Q(x)=(x3−3x2+x+1)−(2x3−x2+3x−4)
=x3−3x2+x+1−2x3+x2−3x+4=x3−3x2+x+1−2x3+x2−3x+4
=−x3−2x2−2x+5=−x3−2x2−2x+5.
b) Thay x=1x=1 vào hai đa thức ta có:
P(1)= 13−3.12+1+1=0P(1)= 13−3.12+1+1=0
Q(1)= 2.13−12+3.1−4=0Q(1)= 2.13−12+3.1−4=0
Vậy x=1x=1 là nghiệm của cả hai đa thức P(x)P(x) và Q(x)Q(x).

`x/(-4) = (-11)/2`
`=> 2x=-4.(-11)`
`=> 2x=44`
`=>x=44:2`
`=>x=22`
`---`
`(15-x)/(x+9) =3/5`
`=> (15-x).5=(x+9).3`
`=> 75-5x =3x+27`
`=> -5x -3x=27 -75`
`=> -8x=-48`
`=>x=-48:(-8)`
`=>x=6`
a) x−4=−112−4x=2−11
x=(−11).(−4)2x=2(−11).(−4)
x=22x=22.
b) 15−xx+9 =35x+915−x =53
(15−x).5 =(x+9).3(15−x).5 =(x+9).3
75−5x =3x+2775−5x =3x+27
8x=488x=48
x=6x=6.

Gọi chiều dài là x, chiều rộng là y ( x,y > 0)
Nửa chu vi hình chữ nhật là 60 : 2 = 30 (cm)
Theo bài ra ta có: \(\dfrac{x}{y}\) = \(\dfrac{2}{3}\) ⇒ \(\dfrac{x}{2}\) = \(\dfrac{y}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{2}\) = \(\dfrac{y}{3}\) = \(\dfrac{x+y}{2+3}\) = \(\dfrac{30}{5}\) = 6
x = 6.2 = 12
y = 6.3 = 18
Diện tích hình chữ nhật : 18 x 12 = 216 (m2)
Kết luận : diện tích hình chữ nhật 216 m2

tam giác ABC cân tại A nên
\(\widehat{B}\) = \(\widehat{C}\)
=> \(\widehat{ABM}\) = \(\widehat{ACN}\) (1)
AB = AC (2)
\(\widehat{BAM}\) = \(\widehat{CAN}\) = 900 (3)
Kết hợp (1); (2); (3) ta có : Δ BAM = Δ CAN ( g-c-g)
=> BM = CN
BM = BN + MN = MN + CM
⇒ BN = CM
\(\widehat{BAN}\) + \(\widehat{NAC}\) = \(\widehat{BAC}\) = 1200
⇒ \(\widehat{BAN}\) = 1200 - \(\overline{NAC}\) = 1200 - 900 = 300
\(\widehat{ABN}\) = ( 1800 - 120 0 ) : 2 = 300 = \(\widehat{BAN}\) ⇒Δ ANB cân tại N 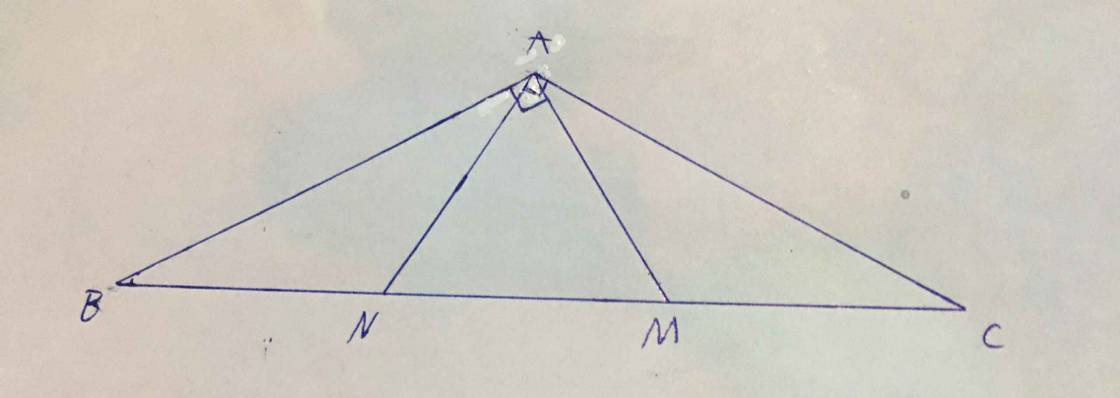

Gọi số máy cày của đội 1, đội 2, đội 3 lần lượt là : x, y, z (x,y,z \(\in\)N)
Theo bài ra ta có : 5x = 6y = 8z
6y = 8z => \(\dfrac{y}{8}\) = \(\dfrac{z}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{y}{8}\) = \(\dfrac{z}{6}\) = \(\dfrac{y-z}{8-6}\) = \(\dfrac{5}{2}\)
y = \(\dfrac{5}{2}\) x 8 = 20
z = \(\dfrac{5}{2}\) x 6 = 15
x = 6 x 20 : 5 = 24
Kết luận : Số máy cày của đội 1, đội 2, đội 3 lần lượt là 24 máy; 20 máy; 15 máy.
Gọi số máy cày của ba đội lần lượt là xx, yy, zz (máy).
Vì diện tích cày là như nhau nên số máy cày và thời gian là hai đại lượng tỉ lệ nghịch.
Nên x.5=y.6=z.8⇒x24=y20=z15x.5=y.6=z.8⇒24x=20y=15z.
Đội thứ hai có nhiều hơn đội thứ ba 55 máy nên y−z=5y−z=5.
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
x24=y20=z15=y−z20−15=55=124x=20y=15z=20−15y−z=55=1
Suy ra x=24x=24; y=20y=20; z=15z=15.

Ta có:
\(2x=5y\) hay \(\dfrac{x}{5}=\dfrac{y}{2}\)
Áp dụng tính chất cơ bản của phân số, ta có:
\(\dfrac{x}{5}=\dfrac{y}{2}\Leftrightarrow\dfrac{3x}{3\cdot5}=\dfrac{4y}{4\cdot2}\)
\(\Rightarrow\dfrac{3x}{15}=\dfrac{4y}{8}\)
Áp dụng tính chất cơ bản của phân số, ta có:
\(\dfrac{3x}{15}=\dfrac{4y}{8}=\dfrac{3x+4y}{15+8}=\dfrac{46}{23}=2\)
\(\Rightarrow x=2\cdot5=10\)
\(\Rightarrow y=2\cdot2=4\)

a, \(\dfrac{x}{-3}\)= \(\dfrac{7}{4}\) ⇒ x = \(\dfrac{7}{4}\)x (-3) ⇒ x = - \(\dfrac{21}{4}\)
b, \(\dfrac{x+9}{15-x}\) = \(\dfrac{2}{3}\) ⇒ 3(x+9) = 2( 15-x) ⇒ 3x + 27 = 30 - 2x
⇒ 3x + 2x = 30 - 27 ⇒
5x = 3 ⇒ x = 3 : 5 ⇒ x = \(\dfrac{3}{5}\)
Trước tiên, chúng ta cần có lý thuyết về biến đổi phân số.
\(\dfrac{b-a}{a\cdot b}=\dfrac{1}{a}-\dfrac{1}{b}\)
Ta có:
\(S=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2017\cdot2018}\)
\(S=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2017}-\dfrac{1}{2018}\)
\(S=1+\left(-\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+...-\dfrac{1}{2018}\)
\(S=1-\dfrac{1}{2018}\)
\(S=\dfrac{2017}{2018}\)
=1/1.2+1/2.3+1/3.4+...1/2017.2018
=1/1-1/2+1/2-1/3+1/3-1/4+...+1/2017-1/2018
=1-1/2018
=2018/2018-1/2018
=2017/2018