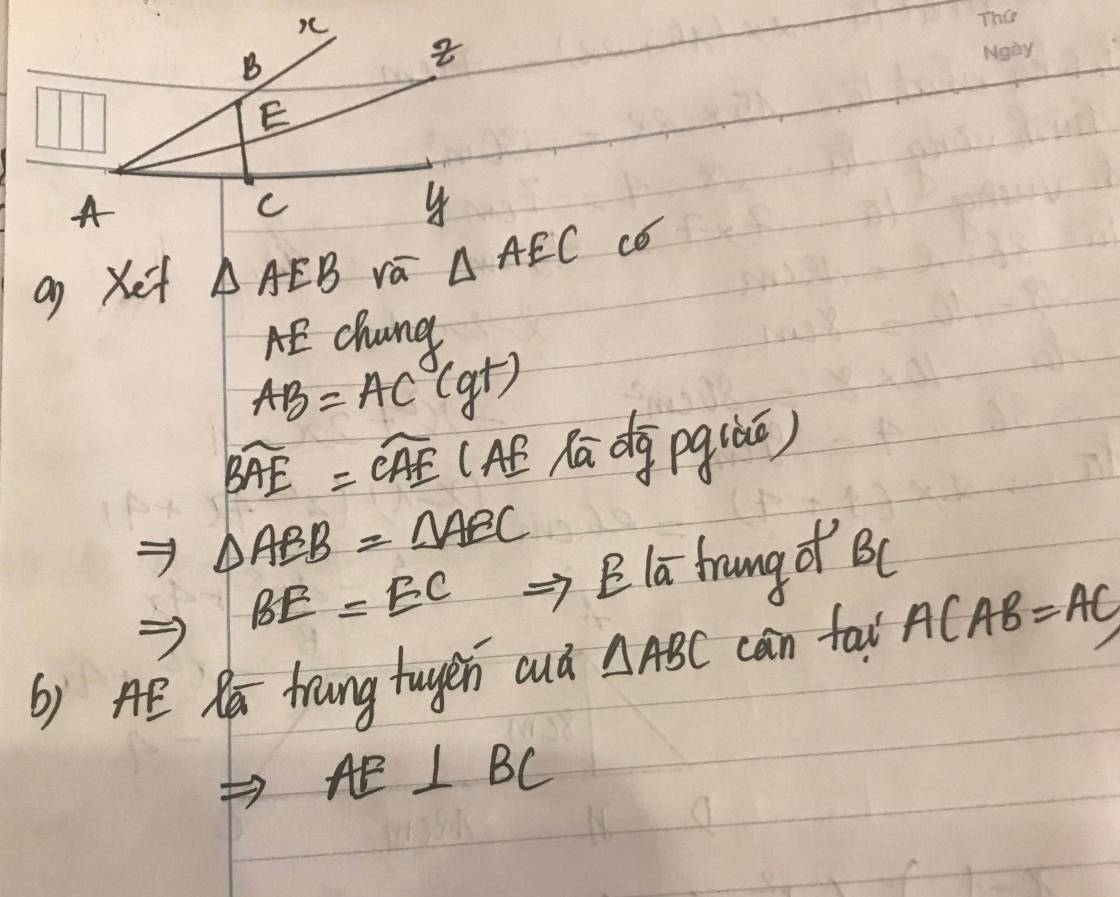
cho góc xAy nhọn. trên Ax lấy điểm B,trên By lấy điểm C sao cho AB=AC. Vẽ tia phân giác của góc A cắt BC tại E.CMR:
a,E là trung điểm của BC
b,OE vuông BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nếu n là số lẻ n có dạng : 2k + 1 ( k\(\in\) N)
A = 2018 + ( 2k+ 1+ 1)2
A = 2018 + (2k+2)2
A = 2018 + 4.( k+1)2 ⇒ A ⋮ 2 Nếu A là số chính phương
⇒ A ⋮ 4 ( tính chất 1 số chính phương )
⇒ 2018 ⋮ 4 ( vô lý)
Nếu n là số chẵn n =2k ( k \(\in\) N)
A = 2018 + ( 2k + 1)2;
2k + 1 không chia hết cho 4 ⇒ ( 2k+1)2 : 4 dư 1 ( tc của 1 số chính phương)
A = 2018 + ( 2k + 1)2 : 4 dư 3 ⇒ A không phải là số chính phương vì một số chính phương chia 4 chỉ có thể dư 0 hoặc 1.
Vậy không thể tồn tại n để 2018 + ( n +1)2 là số chính phương
Gỉa sử 2018 + \(n^2\) là số chính phương => 2018 + \(n^2\) = \(a^2\) ( a là số tự nhiên )
=> 2018 = \(a^2\)- \(n^2\) = (a - n)(a + n)
Ta có: (a + n) - (a - n) = a + n - a +n = 2n ( chia hết cho 2 )
\(\Rightarrow\) 2 số m - n và m + n phải có cùng tính chẵn lẻ
Mà 2018 = 1.2018 = 2.1009 với các cặp số (1;2018) và (2;1009) đều không cùng tính chẵn lẻ
Vậy ta kết luận: 2018 + n^2 không là số chính phương

A = 7 + 72 + 73 + .........+ 7n-1 + 7n
7A = 72 + 73 +..........+ 7n-1 + 7n + 7n-1
7A - A = 7n+1 - 7
6A = ( 7n+1 - 7)
A = (7n+1 - 7) : 6

ta có : 803 là số lẻ
=> ( 50a + 7b + 3 )( 50^a + 50a + b ) là số lẻ
=> 50a + 7b + 3 và 50^a + 50a + b là số lẻ
TH1 : nếu a khác 0
=> 50^a + 50a là là số chẵn
mà 50^a + 50a + b là số lẻ ( theo trên )
=> b lẻ
=> 50b + 3 chẵn
=> 50a + 7b + 3 chẵn ( loại )
TH2 : a = 0
=> (7b+3)(b+1) = 803 = 1. 803 = 11.73
vì b thuộc N
=> 7b + 3 > b+1
do đó
7b + 3 = 803 và b +1 = 1 => loại
hoặc 7b+3 = 73 và b +1 = 11 => b = 50
vậy a = 0 và b = 100