bài 16 số cây trồng của cả 3 lớp 7a,7b,7c lần lượt tỉ lệ vs các số 2,3,5 tính số cây trồng của mỗi lớp , biết rằng cả ba lớp trồng đc tất cả là 50 cây
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(x^2-xy-5x=-4y-9\)
\(\Leftrightarrow x^2-5x+4-y\left(x-4\right)=-5\)
\(\Leftrightarrow\left(x-4\right)\left(x-1\right)-y\left(x-4\right)=-5\)
\(\Leftrightarrow\left(x-4\right)\left(x-1-y\right)=-5\)
Bảng giá trị:
| x-4 | -5 | -1 | 1 | 5 |
| x-1-y | 1 | 5 | -5 | -1 |
| x | -1 | 3 | 5 | 9 |
| y | -3 | -3 | 9 | 9 |
Vậy các cặp (x;y) nguyên thỏa mãn là: \(\left(-1;-3\right);\left(3;-3\right);\left(5;9\right);\left(9;9\right)\)

gọi số thứ nhất là a, số thứ 2 là b, số thứ 2 sau khi thêm 3 đơn vị là b', ta có:
\(\dfrac{a}{b}=\dfrac{4}{3};\dfrac{a}{b'}=\dfrac{5}{4}\)
\(\Leftrightarrow\dfrac{a}{b}=\dfrac{20}{15};\dfrac{a}{b'}=\dfrac{20}{16}\)
\(\Rightarrow\dfrac{b}{b'}=\dfrac{15}{16}\)
\(\Rightarrow16b=15b'\)
\(\Leftrightarrow16b=15\left(b+3\right)\)
\(\Leftrightarrow16b=15b+45\)
\(\Leftrightarrow16b-15b=45\)
\(\Leftrightarrow b=45\)
\(\Rightarrow a=45:3.4=60\)
\(\Rightarrow a+b=45+60=105\)
~HT~

Do t tỉ lệ thuận với z theo tỉ lệ a \(\Rightarrow\dfrac{t}{z}=a\) \(\Rightarrow t=z.a\)
Do z tỉ lệ thuận x theo hệ số tỉ hệ b \(\Rightarrow\dfrac{z}{x}=b\) \(\Rightarrow x=\dfrac{z}{b}\)
Do y tỉ lệ thuận với x theo hệ số tỉ lệ c \(\Rightarrow\dfrac{y}{x}=c\)
Vậy t tỉ lệ thuận với x theo hệ số tỉ lệ là:
\(\dfrac{t}{x}=\dfrac{z.}{\dfrac{z}{b}}=ab\)
x tỉ lệ thuận với z theo hệ số tỉ lệ là:
\(\dfrac{x}{z}=\dfrac{1}{\dfrac{z}{x}}=\dfrac{1}{b}\)

a) \(2x=5y\Leftrightarrow\dfrac{x}{5}=\dfrac{y}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{x+y}{5+2}=\dfrac{-21}{7}=-3\)
Khi đó: \(\left\{{}\begin{matrix}\dfrac{x}{5}=-3\\\dfrac{y}{2}=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3.5=-15\\y=-3.2=-6\end{matrix}\right.\)
\(\Rightarrow O=x^2-xy+2y=\left(-3\right)^2-\left(-15\right).\left(-6\right)+2.\left(-6\right)=9-90-12=-93\)
b)
Đặt \(\dfrac{x}{2}=\dfrac{y}{5}=k\Rightarrow\left\{{}\begin{matrix}x=2k\\y=5k\end{matrix}\right.\)
\(\Rightarrow2k.5k=90\\ \Leftrightarrow10k^2=90\\ \Leftrightarrow k^2=9\\ \Leftrightarrow\left[{}\begin{matrix}k=-3\\k=3\end{matrix}\right.\)
Nếu k = -3
\(\Rightarrow\left\{{}\begin{matrix}x=-3.2=-6\\y=-3.5=-15\end{matrix}\right.\)
\(\Rightarrow Q=-93\)
Nếu k = 3
\(\Rightarrow\left\{{}\begin{matrix}x=3.2=6\\y=3.5=15\end{matrix}\right.\)
\(\Rightarrow Q=6^2-6.15+2.15=-24\)

Bài 1:
a. $y=ax$
Thay $x=-9; y=27$ thì: $27=a(-9)$
$\Rightarrow a=-3$
Công thức liên hệ giữa $y$ và $x$: $y=-3x$
b.
Khi $x=-4$ thì $y=-3x=-3(-4)=12$
Khi $x=0,25$ thì $y=-3.0,25=-0,75$
Khi $x=\frac{1}{3}$ thì $y=-3.\frac{1}{3}=-1$
c. $y=-3x\rightarrow x=\frac{-y}{3}$
Khi $y=-2$ thì $x=\frac{-(-2)}{3}=\frac{2}{3}$
Khi $y=0$ thì $x=\frac{-(0)}{3}=0$
Khi $y=\frac{3}{5}$ thì $x=\frac{-3}{5.3}=\frac{-1}{5}$
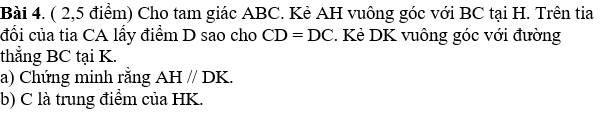
 Giúp mình ;)
Giúp mình ;)



gọi `3` lớp `7A;7B;7C` trồng cây lần lượt là `a,b,c` ( a;b;c ∈ N* )
Theo đề ra ta có : `a/2=b/3=c/5` và `a+b+c=50`
ADTC dãy tỉ số bằng nhau ta có :
`a/2=b/3=c/5 =(a+b+c)/(2+3+5)= 50/ 10=5`
`=> a/2=5=>a=2.5=10`
`=>b/3=5=>b=5.3=15`
`=>c/5=5=>c=5.5=25`
vậy ...