Để A ⋮ B thì:

3n ≤ 9 và 2n ≥ 4

n ≤ 3 và n ≥ 2

n = 2 hoặc n = 3

3\(x\)(- \(\dfrac{4}{3}\)\(x\) + 1) - 4\(x\).(\(x\) - 2) = 10

-4\(x^2\) + 3\(x\) - 4\(x^2\) + 3\(x\) + 8\(x\) = 10

-8\(x^2\) + 14\(x\) - 10 = 0

4\(x^2\) + 7\(x\) - 5 = 0

4.(\(x^2\) + 2.\(\dfrac{7}{8}\) + \(\dfrac{49}{64}\)) - \(\dfrac{129}{16}\) = 0

4.(\(x\) + \(\dfrac{7}{8}\))²  = \(\dfrac{129}{16}\)

   (\(x\) + \(\dfrac{7}{8}\))² =  \(\dfrac{129}{16}\)

    \(x\)           = \(\dfrac{\pm\sqrt{129}-7}{8}\)

Thực hiện phép chia \(f(x)\) cho \(x-1\), ta được:

\(f(x)=(x-1)\cdot Q(x)+r\\\Rightarrow f(1)=(1-1)\cdot Q(1)+r\\\Rightarrow f(1)=r\\\Rightarrow 1^{100}+1^{99}+1^{98}+1^{97}+...+1+1=r\\\Rightarrow r=101(101.chữ.số.1)\)

Vậy số dư của phép chia $f(x)$ cho $(x-1)$ là 101.

B:4x = 2xy^2 + 3xy - 5x

=> B = 4x(2xy^2 + 3xy - 5x )

= 8x^2y^2 + 12x^2y - 20x^2

    36\(x^3\).y⁴.z² : 6\(x^2\).y⁴.z

=  (36 : 6).(\(x^3\).\(x^2\)).(y⁴.y⁴).z

= 6.\(x^5\).y⁸.z

\(\dfrac{36x^3y^4z^2}{6x^2y^4z}=6xz\)

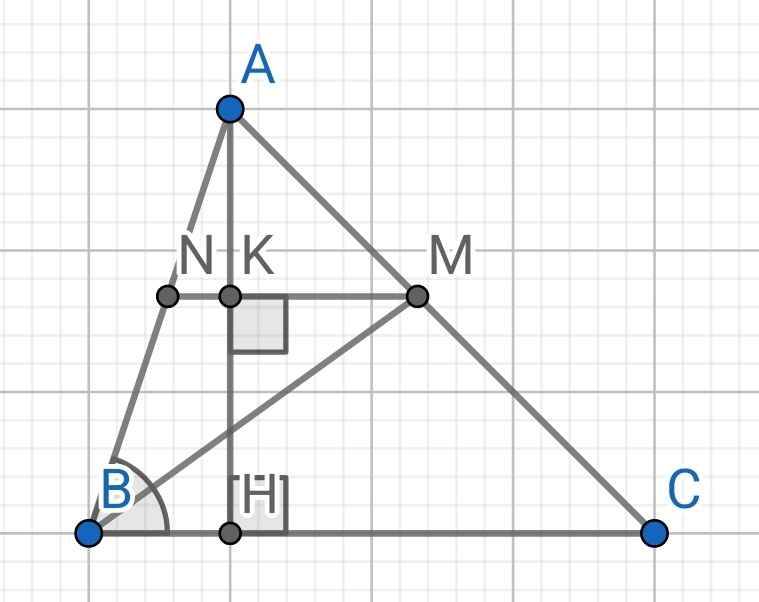 a) Do MN ⊥ AH (gt)

BC ⊥ AH (AH là đường cao)

⇒ MN // BC

Tứ giác BCMN có:

MN // BC (cmt)

⇒ BCMN là hình thang

b) Do MN // BC (cmt)

⇒ ∠MBC = ∠BMN (so le trong)  (1)

Lại có:

BM là tia phân giác của ∠ABC (gt)

⇒ ∠MBC = ∠MBN  (2)

Từ (1) và (2) ⇒ ∠MBN = ∠BMN

∆BMN có:

∠MBN = ∠BMN (cmt)

⇒ ∆BMN cân tại N

⇒ BM = MN

a) (1/3 x²y)(2xy³)

= (1/3 . 2).(x².x).(y.y³)

= 2/3 x³y⁴

Hệ số: 2/3

Phần biến: x³y⁴

Bậc: 7

b) 1/4 x³y .(-2x³y⁴)

= [1/4 . (-2)].(x³.x³).(y.y⁴)

= -1/2 x⁶y⁵

Hệ số: -1/2

Phần biến: x⁶y⁵

Bậc: 11

c) -xy.(2x³y⁴).(-5/4x²y³)

= [-2.(-5/4)].(x.x³.x²).(y.y⁴.y³)

= 5/2 x⁶y⁸

Hệ số: 5/2

Phần biến: x⁶y⁸

Bậc: 14

Giúp t vs ạ