
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Lời giải
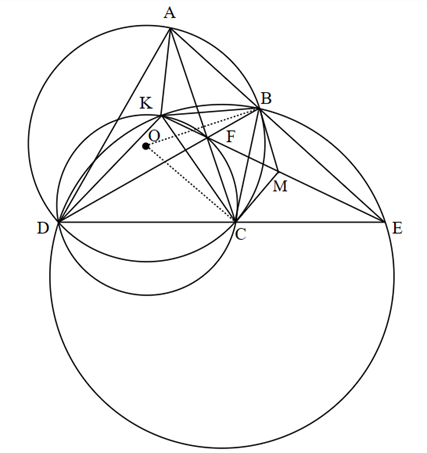
a) Vì điểm K nằm trên đường tròn ngoại tiếp ΔBDE nên tứ giác DKBE nội tiếp đường tròn
Suy ra ˆBEK=ˆBDK𝐵𝐸𝐾^=𝐵D𝐾^ (2 góc nội tiếp cùng chắn cung BK)
Hay ˆAEK=ˆFDK𝐴𝐸𝐾^=FD𝐾^
Vì tứ giác DKFC nội tiếp đường tròn nên ˆFCK=ˆFDK𝐹𝐶𝐾^=FD𝐾^
Suy ra ˆAEK=ˆFCK𝐴𝐸𝐾^=FC𝐾^, hay ˆAEK=ˆACK𝐴𝐸𝐾^=AC𝐾^
Do đó tứ giác AKCE nội tiếp đường tròn
Suy ra ˆKAE+ˆKCE=180∘𝐾AE^+𝐾𝐶𝐸^=180∘
Mà ˆKCD+ˆKCE=180∘𝐾𝐶D^+𝐾𝐶𝐸^=180∘ (hai góc kề bù)
Do đó ˆKAE=ˆKCD𝐾AE^=𝐾𝐶D^ hay ˆKAB=ˆKCD𝐾AB^=𝐾𝐶D^
Do tứ giác BKDE nội tiếp đường tròn nên ˆKDE+ˆKBE=180∘𝐾𝐷E^+𝐾𝐵𝐸^=180∘
Mà ˆKBA+ˆKBE=180∘𝐾𝐵𝐴^+𝐾𝐵𝐸^=180∘ (hai góc kề bù)
Do đó ˆKDE=ˆKBA𝐾𝐷E^=𝐾𝐵𝐴^ hay ˆKBA=ˆKDCKBA^=𝐾𝐷𝐶^
Xét ΔDKC và ΔBKA có:
ˆKBA=ˆKDCKBA^=𝐾𝐷𝐶^ (chứng minh trên)
ˆKAB=ˆKCD𝐾AB^=𝐾𝐶D^ (chứng minh trên)
Suy ra (g.g)
Do đó KCKA=KDKB𝐾𝐶𝐾A=𝐾D𝐾𝐵
Hay KCKD=KAKB𝐾𝐶𝐾𝐷=𝐾𝐴𝐾𝐵
Ta có: ˆBKD=ˆDKC+ˆBKC𝐵𝐾D^=𝐷𝐾𝐶^+𝐵𝐾𝐶^; ˆAKC=ˆBKA+ˆBKC𝐴𝐾𝐶^=𝐵𝐾𝐴^+𝐵𝐾𝐶^
Mà ˆDKC=ˆBKA𝐷𝐾𝐶^=𝐵𝐾A^, suy ra ˆDKB=ˆCKA𝐷𝐾𝐵^=𝐶𝐾A^
Xét ΔKBD và ΔKAC có:
ˆDKB=ˆCKA𝐷𝐾𝐵^=𝐶𝐾A^ (chứng minh trên)
KCKD=KAKB𝐾𝐶𝐾𝐷=𝐾𝐴𝐾𝐵 (chứng minh trên)
Suy ra (c.g.c)
Do đó ˆKBD=ˆKAC𝐾𝐵D^=𝐾𝐴𝐶^
Hay ˆKBF=ˆKAF𝐾𝐵𝐹^=𝐾𝐴𝐹^
Suy ra tứ giác AKFB nội tiếp đường tròn
Do đó ˆBKF=ˆBAF𝐵𝐾𝐹^=BAF^ (2 góc nội tiếp chắn cung BF)
Suy ra ˆBKF=ˆBAC=ˆBDC𝐵𝐾𝐹^=𝐵𝐴𝐶^=𝐵D𝐶^ (do ˆBAC,ˆBDC𝐵𝐴𝐶^,𝐵D𝐶^ cùng chắn cung BC) (1)
Ta có: ˆBDC=ˆFDC=ˆFKC𝐵D𝐶^=𝐹D𝐶^=𝐹𝐾𝐶^ (cùng chắn cung FC) (2)
Xét ΔBMC có ˆMBC+ˆMCB+ˆBMC=180∘𝑀𝐵𝐶^+𝑀𝐶𝐵^+𝐵𝑀𝐶^=180∘ (tổng ba góc trong một tam giác)
Mà ˆMBC=ˆBAC,ˆMCB=ˆBDC𝑀𝐵𝐶^=𝐵𝐴𝐶^,𝑀𝐶𝐵^=𝐵D𝐶^(Góc tạo bởi tiếp tuyến và dây cung)
Suy ra ˆBAC+ˆBDC+ˆBMC=180∘𝐵𝐴𝐶^+𝐵𝐷𝐶^+𝐵𝑀𝐶^=180∘ (3)
Từ (1); (2) và (3) suy ra ˆBKF+ˆFKC+ˆBMC=180∘𝐵𝐾𝐹^+𝐹𝐾𝐶^+𝐵𝑀𝐶^=180∘
Hay ˆBKC+ˆBMC=180∘𝐵𝐾𝐶^+𝐵𝑀𝐶^=180∘
Do đó tứ giác BKCM nội tiếp đường tròn
b) Ta có ˆBKF=ˆBDC𝐵𝐾𝐹^=𝐵D𝐶^ (chứng minh câu a)
Suy ra ˆBKF=ˆBDE=ˆBKE𝐵𝐾𝐹^=𝐵DE^=𝐵𝐾𝐸^ (Do tứ giác DKBE nội tiếp đường tròn)
Mà 2 điểm F và E nằm cùng phía so với BK
Suy ra 3 điểm K; F; E thẳng hàng
Hay F nằm trên KE (*)
Vì ˆBKF=ˆBAC,ˆCKF=ˆBDC,ˆBAC=ˆBDC𝐵𝐾𝐹^=𝐵𝐴𝐶^,𝐶𝐾𝐹^=𝐵D𝐶^,𝐵𝐴𝐶^=𝐵D𝐶^
Nên ˆBKF=ˆCKF𝐵𝐾𝐹^=𝐶𝐾𝐹^
Suy ra ˆBKE=ˆCKE𝐵𝐾𝐸^=𝐶𝐾𝐸^ (Do K; F; E thẳng hàng)
Do đó KE là phân giác của ˆBKC𝐵𝐾𝐶^ (4)
Xét (O) có MB, MC là 2 tiếp tuyến cắt nhau tại M
Nên MB = MC
Do đó tam giác MBC cân tại M
Suy ra ˆMBC=ˆMCB𝑀𝐵𝐶^=𝑀𝐶𝐵^
Xét tứ giác BKCM nội tiếp đường tròn có ˆMBC=ˆMKC,ˆMCB=ˆMKB𝑀𝐵𝐶^=𝑀𝐾𝐶^,𝑀𝐶𝐵^=𝑀𝐾𝐵^
Suy ra ˆMKC=ˆMKB𝑀𝐾𝐶^=𝑀𝐾𝐵^
Do đó KM là phân giác của ˆBKC𝐵𝐾𝐶^ (5)
Từ (4) và (5) suy ra 3 điểm K; M; E thẳng hàng hay M nằm trên KE (**)
Từ (*) và (**) suy ra 3 điểm E; M; F thẳng hàng
Vậy 3 điểm E; M; F thẳng hàng.

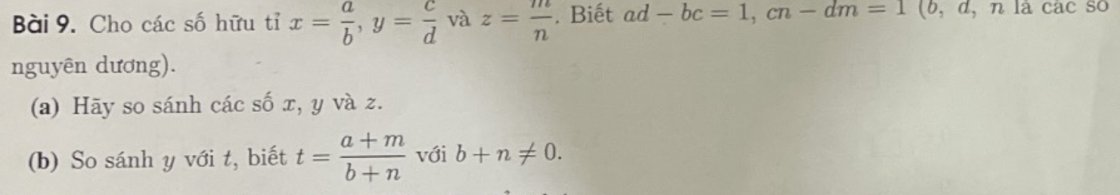 mn lm giup e vs
mn lm giup e vs